The following problems require the use of implicit differentiation. Implicit differentiation is nothing more than a special case of the well-known chain rule for derivatives. The majority of differentiation problems in first-year calculus involve functions y written EXPLICITLY as functions of x . For example, if
![]() ,
,
then the derivative of y is
![]() .
.
However, some functions y are written IMPLICITLY as functions of x . A familiar example of this is the equation
x2 + y2 = 25 ,
which represents a circle of radius five centered at the origin. Suppose that we wish to find the slope of the line tangent to the graph of this equation at the point (3, -4) .

How could we find the derivative of y in this instance ? One way is to first write y explicitly as a function of x . Thus,
x2 + y2 = 25 ,
y2 = 25 - x2 ,
and
![]() ,
,
where the positive square root represents the top semi-circle and the negative square root represents the bottom semi-circle. Since the point (3, -4) lies on the bottom semi-circle given by
![]() ,
,
the derivative of y is
![]() ,
,
i.e.,
![]() .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
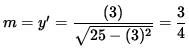 .
.
Unfortunately, not every equation involving x and y can be solved explicitly for y . For the sake of illustration we will find the derivative of y WITHOUT writing y explicitly as a function of x . Recall that the derivative (D) of a function of x squared, (f(x))2 , can be found using the chain rule :
![]() .
.
Since y symbolically represents a function of x, the derivative of y2 can be found in the same fashion :
![]() .
.
Now begin with
x2 + y2 = 25 .
Differentiate both sides of the equation, getting
D ( x2 + y2 ) = D ( 25 ) ,
D ( x2 ) + D ( y2 ) = D ( 25 ) ,
and
2x + 2 y y' = 0 ,
so that
2 y y' = - 2x ,
and
![]() ,
,
i.e.,
![]() .
.
Thus, the slope of the line tangent to the graph at the point (3, -4) is
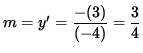 .
.
This second method illustrates the process of implicit differentiation. It is important to note that the derivative expression for explicit differentiation involves x only, while the derivative expression for implicit differentiation may involve BOTH x AND y .
The following problems range in difficulty from average to challenging.
Click HERE to see a detailed solution to problem 1.
Click HERE to see a detailed solution to problem 2.
Click HERE to see a detailed solution to problem 3.
Click HERE to see a detailed solution to problem 4.
Click HERE to see a detailed solution to problem 5.
Click HERE to see a detailed solution to problem 6.
Click HERE to see a detailed solution to problem 7.
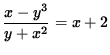 .
.
Click HERE to see a detailed solution to problem 8.
Click HERE to see a detailed solution to problem 9.
Click HERE to see a detailed solution to problem 10.
Click HERE to see a detailed solution to problem 11.
Click HERE to see a detailed solution to problem 12.
Click HERE to see a detailed solution to problem 13.

Click HERE to see a detailed solution to problem 14.

Click HERE to see a detailed solution to problem 15.

Click HERE to see a detailed solution to problem 16.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :