SOLUTION 3: We are given the equation $ x^3+2x-5=0 $. Let function
$$ f(x)=x^3+2x-5 \ \ \ \ and \ choose \ \ \ \ m=0 $$
This function is continuous for all values of $x$ since it is a polynomial.
To establish an appropriate interval consider the graph of this function. (Please note that the graph of the function is not necessary for a valid proof, but the graph will help us understand how to use the Intermediate Value Theorem. On many subsequent problems, we will solve the problem without using the "luxury" of a graph.)
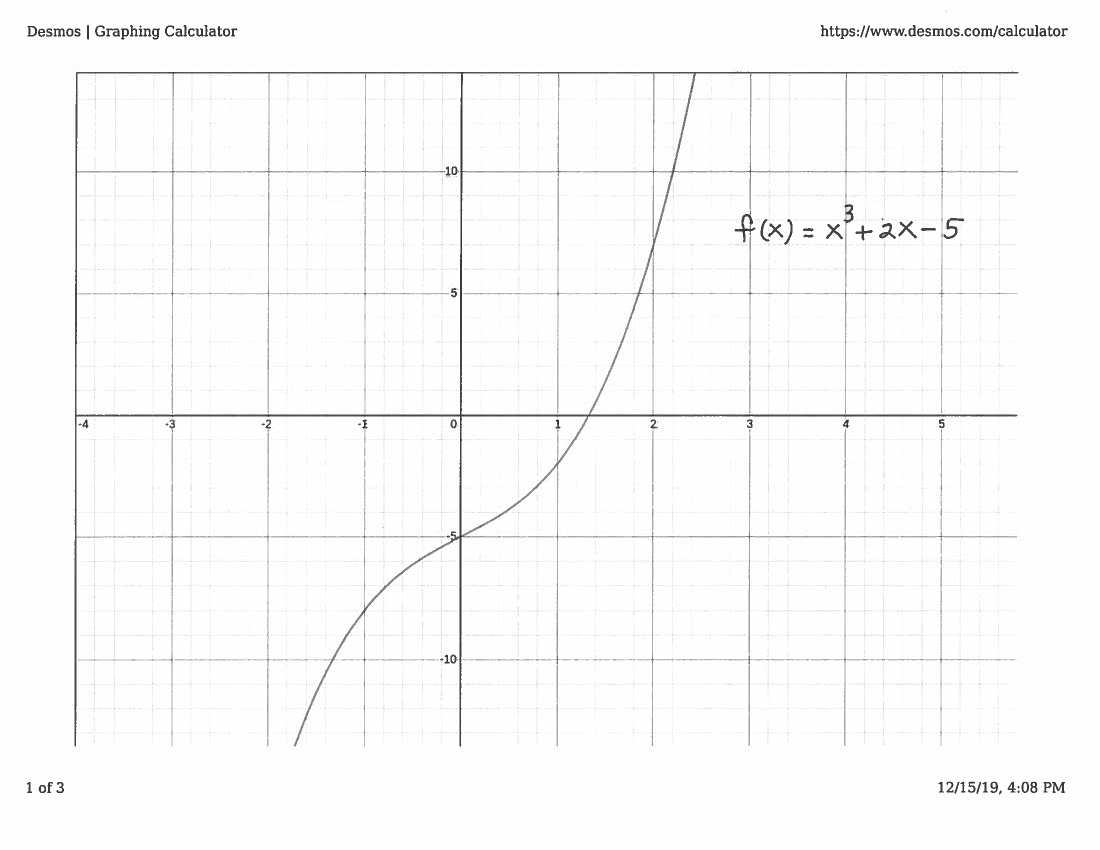
Note that $$ f(1)= (1)^3+2(1)-5= -2<0 \ \ \ \ and \ \ \ \ f(2)= (2)^3+2(1)-5=5>0 $$
so that $$ f(1)=-2 < m < 5=f(2) $$
i.e., $m=0$ is between $ f(1) $ and $ f(2) $. Now choose the interval to be $ \ [1, 2] $.
The assumptions of the Intermediate Value Theorem have now been met, so we can conclude that there is some number $c$ in the interval $[1, 2]$ which satisfies
$$ f(c)=m $$
i.e.,
$$ c^3+2c-5=0 $$
and the equation is solvable.
Click HERE to return to the list of problems.

