SOLUTION 1: We are given the equation $ x^3+x-5=0 $, so let's define function $ f(x) = x^3+x-5$, whose graph is given below.
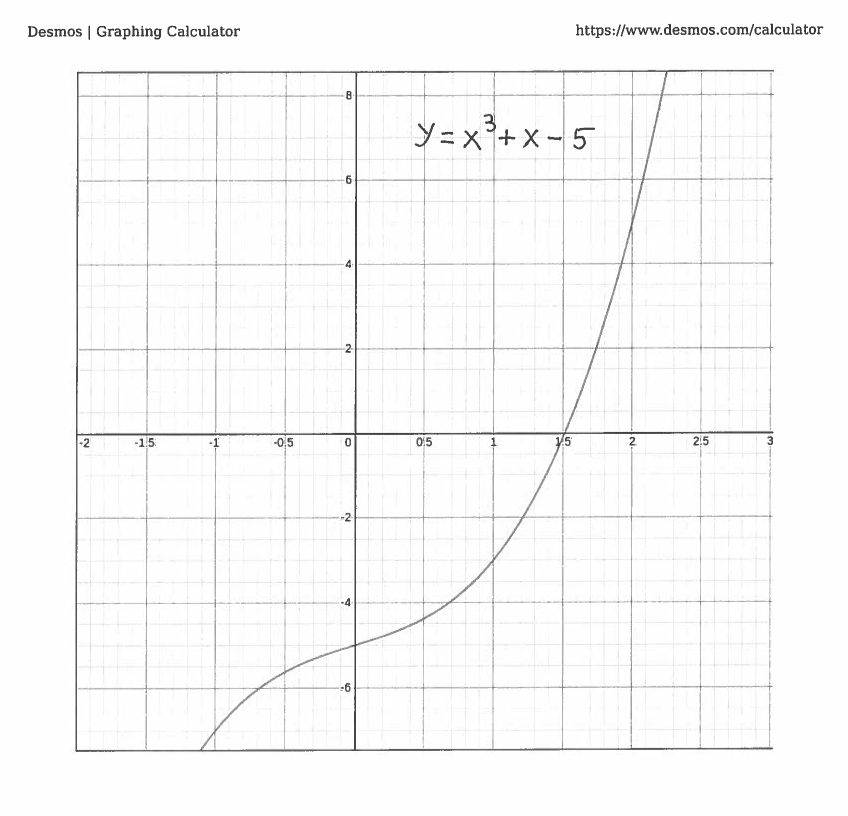
The derivative of $f$ is $ f'(x) = 3x^2+1 $. Now use Newton's Method:
$$ x_{n+1} = x_{n} - { f(x_{n}) \over f'(x_{n}) } \ \ \ \ \longrightarrow $$
$$ x_{n+1} = x_{n} - { x_{n}^3+x_{n}-5 \over 3x_{n}^2+1} \ \ \ \ \longrightarrow $$
(Let's simplify the right-hand side of this equation. First get a common denominator.)
$$ x_{n+1} = x_{n} \ { 3x_{n}^2+1 \over 3x_{n}^2+1 } - { x_{n}^3+x_{n}-5 \over 3x_{n}^2+1} \ \ \ \ \longrightarrow $$
$$ x_{n+1} = { 3x_{n}^3+ x_{n} \over 3x_{n}^2+1 } - { x_{n}^3+x_{n}-5 \over 3x_{n}^2+1} \ \ \ \ \longrightarrow $$
$$ x_{n+1} = { 3x_{n}^3+ x_{n} - ( x_{n}^3+x_{n}-5 ) \over 3x_{n}^2+1 } \ \ \ \ \longrightarrow $$
$$ x_{n+1} = { 2x_{n}^3+5 \over 3x_{n}^2+1 } $$
a.) Let $ x_{0}=0 $. Then using Newton's Method formula we get that
$$ x_{1} = { 2x_{0}^3+5 \over 3x_{0}^2+1 } = { 2(0)^3+5 \over 3(0)^2+1 } = 5 $$
and
$$ x_{2} = { 2x_{1}^3+5 \over 3x_{1}^2+1 } = { 2(5)^3+5 \over 3(5)^2+1 } = { 255 \over 76 } \approx 3.355263158 $$
Using Newton's Method formula for 8 iterations in a spreadsheet results in :

Thus the solution $r$ to the original equation to five decimal places is $ r \approx 1.51598 $.
b.) Let $ x_{0}=1 $. Then using Newton's Method formula we get that
$$ x_{1} = { 2x_{0}^3+5 \over 3x_{0}^2+1 } = { 2(1)^3+5 \over 3(1)^2+1 } = { 7 \over 4} = 1.75 $$
and
$$ x_{2} = { 2x_{1}^3+5 \over 3x_{1}^2+1 } = { 2(1.75)^3+5 \over 3(1.75)^2+1 } = { 1006 \over 652 } \approx 1.54294 $$
Using Newton's Method formula for 5 iterations in a spreadsheet results in :

Thus the solution $r$ to the original equation to five decimal places is $ r \approx 1.51598 $.
c.) Let $ x_{0}=-1 $. Then using Newton's Method formula we get that
$$ x_{1} = { 2x_{0}^3+5 \over 3x_{0}^2+1 } = { 2(-1)^3+5 \over 3(-1)^2+1 } = { 3 \over 4 } =0.75 $$
and
$$ x_{2} = { 2x_{1}^3+5 \over 3x_{1}^2+1 } = { 2(0.75)^3+5 \over 3(0.75)^2+1 } = { 374 \over 172 } \approx 2.17441 $$
Using Newton's Method formula for 7 iterations in a spreadsheet results in :

Thus the solution $r$ to the original equation to five decimal places is $ r \approx 1.51598 $.
Click HERE to return to the list of problems.




