Newton's Method Solution 5

Processing math: 100%

SOLUTION 5: We want to solve the equation

$f(x)=0$ for the function

$f(x) = \cases{ \sqrt{x} , \ if \ x \ge 0 \cr -\sqrt{-x} , \ if \ x<0 \cr }$

It's graph is given here.

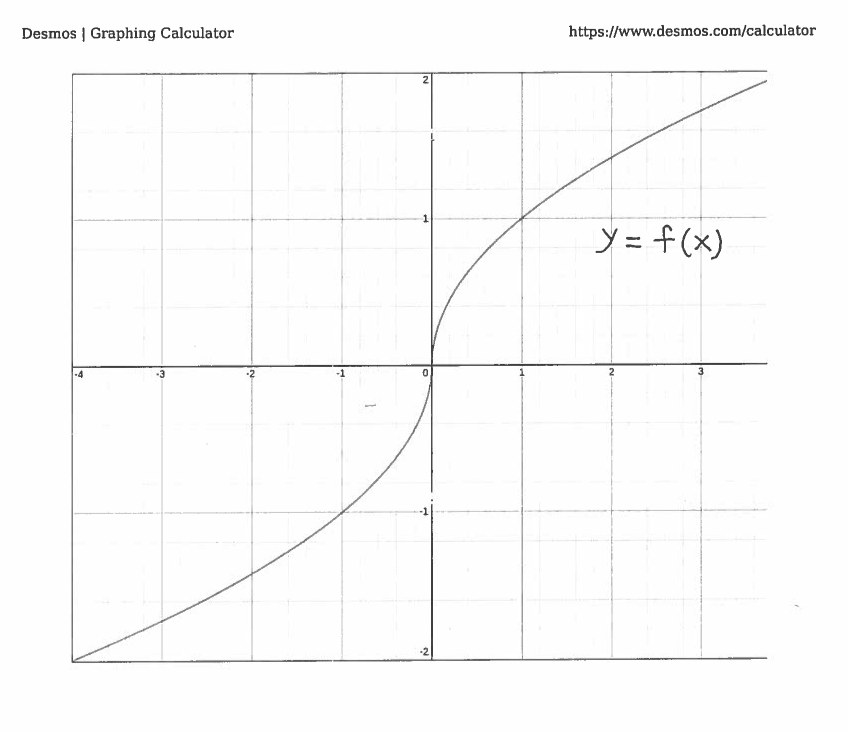
tex2html_wrap_inline125

The derivative of

$f$ is

$f'(x) = { 1 \over 2 }x^{-1/2} = { 1 \over 2 \sqrt{x} } \ \ \ \ \ if \ \ x>0$ and

$f'(x) = { 1 \over 2 }(-x)^{-1/2}(-1) = { -1 \over 2 \sqrt{-x} } \ \ \ \ \ if \ \ x<0$ Now use Newton's Method. If

$x_{n}>0$ then

$x_{n+1} = x_{n} - { f(x_{n}) \over f'(x_{n}) } \ \ \ \ \longrightarrow$

$x_{n+1} = x_{n} - { \sqrt{x_{n}} \over { 1 \over 2 \ \sqrt{x_{n}} } } \ \ \ \ \longrightarrow$

$x_{n+1} = x_{n} - 2 x_{n} \ \ \ \ \longrightarrow$

$x_{n+1} = - x_{n}$ If

$x_{n}<0$ then

$x_{n+1} = x_{n} - { f(x_{n}) \over f'(x_{n}) } \ \ \ \ \longrightarrow$

$x_{n+1} = x_{n} - { \sqrt{-x_{n}} \over { -1 \over 2 \ \sqrt{-x_{n}} } } \ \ \ \ \longrightarrow$

$x_{n+1} = x_{n} + 2(- x_{n}) \ \ \ \ \longrightarrow$

$x_{n+1} = - x_{n}$ We can conclude that Newton's Method formula is

$x_{n+1} = - x_{n}$ for any

$x_{n} \ne 0$ . Begin with the initial guess of

$x_{0}= h>0$ . Using Newton's Method we get that

$x_{1} = - x_{0}= -h \ \ \ \ \longrightarrow$

$x_{2} = - x_{1} = -(-h) = h \ \ \ \ \longrightarrow$

$x_{3} = - x_{2} = -h \ \ \ \ \longrightarrow$

$x_{4} = - x_{3} = -(-h) = h \ \ \ \ \longrightarrow$ etc. It's clear that Newton's Method is trapped in an endless loop, which fails to converge to the solution

$x=0$ . This example shows that Newton's Method sometimes fails to work.

Click HERE to return to the list of problems.