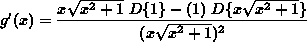
Then
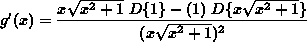
(Apply the product rule in the second part of the numerator. Recall that ![]() .)
.)
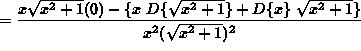
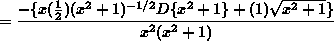
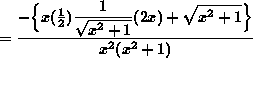
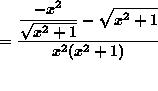
(Begin to simplify the final answer by getting a common denominator in the numerator.)
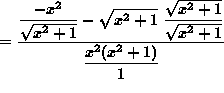
(Simplify the numerator and invert and multiply by the reciprocal of the denominator.)
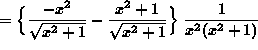
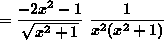
![]()
(Recall that ![]() .)
.)
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 13 : Differentiate 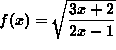 . First apply the chain rule. Then
. First apply the chain rule. Then
![]()
(Now apply the quotient rule and recall that
![]() . Please not that there is a TYPO in the remaining steps of this solution. Every subsequent term (3x+1) should be (3x+2).)
. Please not that there is a TYPO in the remaining steps of this solution. Every subsequent term (3x+1) should be (3x+2).)
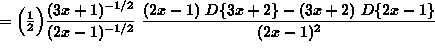
(Recall that
![]() and
and ![]() .)
.)
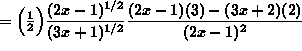
(Recall that
![]() .)
.)
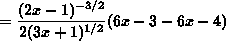
(Please note that there is a TYPO in the final answer. The term (3x+1) should be (3x+2).)
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 14 : Differentiate ![]() .
Recall that
.
Recall that ![]() and apply the chain rule. Then
and apply the chain rule. Then
![]()
(Now apply the quotient rule.)
![]()
![]()
![]()
![]()
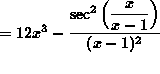 .
.
Click HERE to return to the list of problems.
SOLUTION 15 : Differentiate ![]() . Apply the product rule first. Then
. Apply the product rule first. Then
![]()
(Recall that ![]() and apply the quotient rule.)
and apply the quotient rule.)
![]()
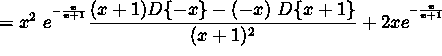
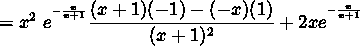
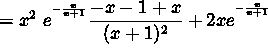
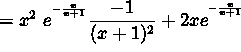
(Begin to simplify your answer by finding a common denominator.)
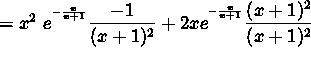
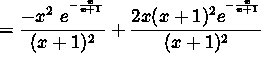
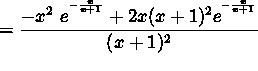
(Factor x and ![]() from the numerator.)
from the numerator.)
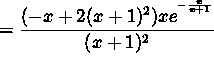
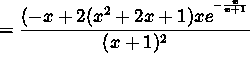
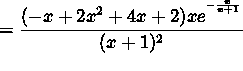
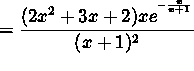 .
.
Click HERE to return to the list of problems.
SOLUTION 16 : Find an equation of the line tangent to the graph of ![]() at x=-1 . If x= -1 then
at x=-1 . If x= -1 then
![]() so that the tangent line passes through the point
(-1, 1 ) . The slope of the tangent line follows from the derivative of y . Then
so that the tangent line passes through the point
(-1, 1 ) . The slope of the tangent line follows from the derivative of y . Then
![]()
![]()
![]()
![]() .
.
The slope of the line tangent to the graph at x = -1 is
![]() .
.
Thus, an equation of the tangent line is
y - 1 = -5 (x - (-1) ) or y = -5x - 4 .
Click HERE to return to the list of problems.
SOLUTION 17 : Find an equation of the line tangent to the graph of ![]() at
at ![]() . If
. If ![]() then
then
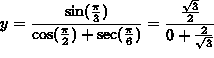
![]() so that the tangent line passes through the point
so that the tangent line passes through the point
![]() . The slope of the tangent line follows from the derivative of y . Then
. The slope of the tangent line follows from the derivative of y . Then
![]()
![]() .
.
There is no need to simpliy this derivative. Just let ![]() in the derivative equation. Thus,
the slope of the line tangent to the graph at
in the derivative equation. Thus,
the slope of the line tangent to the graph at ![]() is
is
m = y'
![]()
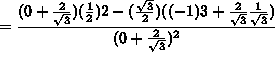
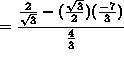
![]()
![]()
![]() .
.
Thus, an equation of the tangent line is
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 18 : Consider the function ![]() .
Solve f'(x) = 0 for x . Solve f''(x) = 0 for x . The first derivative is
.
Solve f'(x) = 0 for x . Solve f''(x) = 0 for x . The first derivative is
![]()
![]()
(Factor out the common terms of 2x and ![]() in the numerator.)
in the numerator.)
![]()
(Recall that 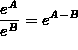 and
and ![]() .)
.)
![]()
![]() .
.
(It is a fact that if ![]() then A = 0 .)
then A = 0 .)
Thus,
2x (1-x) = 0 ,
(It is a fact that if A B = 0 , then A=0 or B = 0 .)
so that
2x = 0 or 1-x = 0 ,
i.e.,
x = 0 or x = 1
are the only solutions to f'(x) = 0 .
The second derivative is
![]()
![]()
![]()
(Factor ![]() from the numerator.)
from the numerator.)
![]()
![]()
![]() .
.
It follows that
![]() ,
,
so that using the quadratic formula we get that
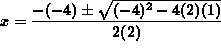
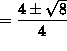
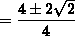
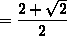 or
or ![]()
are the only solutions to f''(x) = 0 .
Click HERE to return to the list of problems.
SOLUTION 19 : Find all points (x, y) on the graph of ![]() where tangent lines are perpendicular to the line 8x+2y = 1 . Since
where tangent lines are perpendicular to the line 8x+2y = 1 . Since
8x+2y = 1 iff 2y = 1 - 8x iff ![]() ,
,
the slope of this given line is -4. Thus, a tangent line to the graph of f which is perpendicular to 8x+2y = 1 will have slope
![]() .
.
The slope of a tangent line is also given by the derivative
![]()
![]()
![]()
![]() .
.
Thus, equating slopes, it follows that
![]()
iff
![]()
iff
![]()
(Recall that ![]() .)
.)
iff
| 2-x | = 2
iff
![]()
iff
x = 0 or x = 4 .
It follows that there are two distinct tangent lines which are perpendicular to the line 8x+2y = 1 . If x = 0 , then
![]() ,
,
and if x = 4 , then
![]() ,
,
so that the two distinct points of tangency are
( 0, -1/ 2 ) and ( 4, -3/ 2 ) .
Click HERE to return to the list of problems.