![]() ...
...
![]()
be an arbitrary (randomly selected) partition of the interval ![]() , which divides the interval into
, which divides the interval into ![]() subintervals (subdivisions). Let
subintervals (subdivisions). Let
![]() ...
...
![]()
be the sampling numbers (or sampling points) selected from the subintervals. That is,
![]() is in
is in
![]() ,
,
![]() is in
is in
![]() ,
,
![]() is in
is in
![]() , ... ,
, ... ,
![]() is in
is in
![]() ,
,
![]() is in
is in
![]() ,
,
and
![]() is in
is in
![]() .
.
Define the mesh of the partition to be the length of the largest subinterval. That is, let
![]()
for
![]() and define
and define
![]() .
.
The definite integral of ![]() on the interval
on the interval ![]() is most generally defined to be
is most generally defined to be
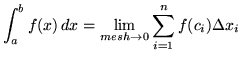 .
.
For convenience of computation, a special case of the above definition uses ![]() subintervals of equal length and sampling points chosen to be the right-hand endpoints of the subintervals. Thus, each subinterval has length
subintervals of equal length and sampling points chosen to be the right-hand endpoints of the subintervals. Thus, each subinterval has length
equation (*)
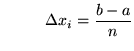
for
![]() and the right-hand endpoint formula is
and the right-hand endpoint formula is
equation (**)
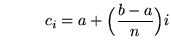
for
![]() . The definite integral of
. The definite integral of ![]() on the interval
on the interval ![]() can now be alternatively defined by
can now be alternatively defined by
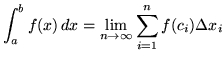 .
.
We will need the following well-known summation rules.
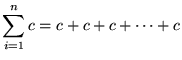 (n times)
(n times) 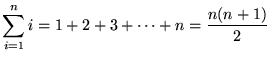
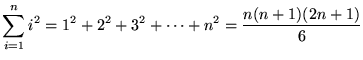
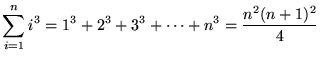
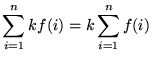 , where
, where 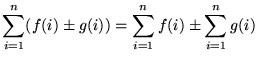
Most of the following problems are average. A few are somewhat challenging. If you are going to try these problems before looking at the solutions, you can avoid common
mistakes by using the formulas given above in exactly the form that they are given. Solutions to the first eight problems will use equal-sized subintervals and right-hand endpoints as sampling points as shown in equations (*) and (**) above.
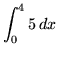 .
.
Click HERE to see a detailed solution to problem 1.
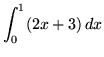 .
.
Click HERE to see a detailed solution to problem 2.
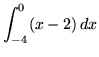 .
.
Click HERE to see a detailed solution to problem 3.
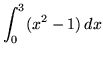 .
.
Click HERE to see a detailed solution to problem 4.
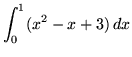 .
.
Click HERE to see a detailed solution to problem 5.
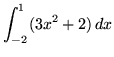 .
.
Click HERE to see a detailed solution to problem 6.
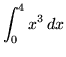 .
.
Click HERE to see a detailed solution to problem 7.
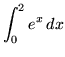 .
.
Click HERE to see a detailed solution to problem 8.
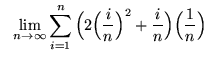 .
.
Click HERE to see a detailed solution to problem 9.
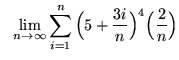 .
.
Click HERE to see a detailed solution to problem 10.
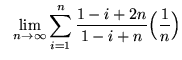 .
.
Click HERE to see a detailed solution to problem 11.
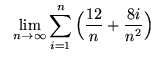 .
.
Click HERE to see a detailed solution to problem 12.
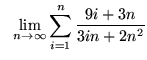 .
.
Click HERE to see a detailed solution to problem 13.
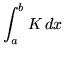 , where
, where
Click HERE to see a detailed solution to problem 14.
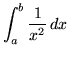 . Use an arbitrary partition
. Use an arbitrary partition
Click HERE to see a detailed solution to problem 15.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :