SOLUTION 4: Consider the region enclosed by the graph of the line $ y= {b \over h}x $ on the interval $ [0, h] $. Revolving this region about the $x$-axis will create the appropriate right circular cone of height $h$ and base radius $b$. Here are a carefully labeled sketch of the region, a rough sketch of the resulting Solid of Revolution, and a circular cross-section at $x$ of radius $r$. It is IMPORTANT to mark BOTH $x$ and $r$ in the sketch of the region !!!
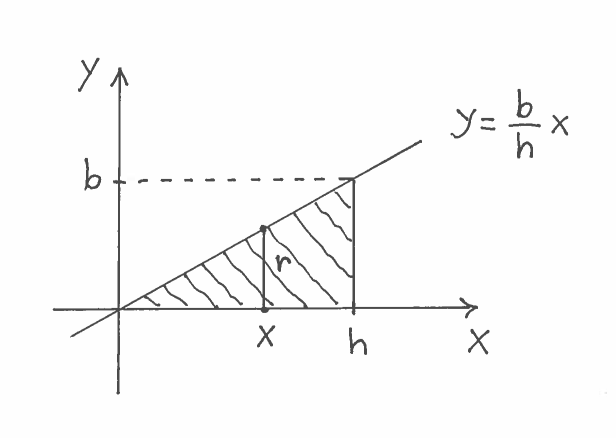 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $
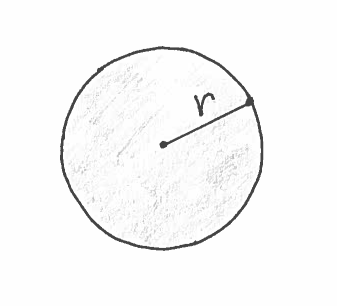
The area of the circular cross-section is
$$ A(x)= \pi r^2 = \pi ({b \over h}x )^2 $$
Thus the total volume of this Solid of Revolution is
$$ Volume = \int_{0}^{h} \pi ({b \over h}x )^2 \ dx $$
$$ = \int_{0}^{h} \pi {b^2 \over h^2}x^2 \ dx $$
$$ = \pi {b^2 \over h^2} \cdot {1 \over 3}x^3 \Big|_{0}^{h} $$
$$ = \pi {b^2 \over h^2} \cdot {1 \over 3}h^3 $$
$$ = {1 \over 3} \pi b^2 h $$
i.e.,
$$ Volume = {1 \over 3} \pi b^2 h $$
Click HERE to return to the list of problems.
 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $

 $ \ \ \ $
$ \ \ \ $
 $ \ \ \ $
$ \ \ \ $
