![]() ,
,
where ![]() represents the natural (base e) logarithm of x and
represents the natural (base e) logarithm of x and
![]() ,
,
where ![]() represents the inverse function of
represents the inverse function of ![]() .
These formulas lead immediately to the following indefinite integrals :
.
These formulas lead immediately to the following indefinite integrals :
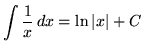 ,
,
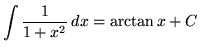 .
.
Because the integral
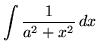 ,
,
where a is any positive constant, appears frequently in the following set of problems, we will find a formula for it now using u-substitution so that we don't have to do this simple process each time. Begin by rewriting the function. Then
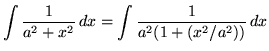
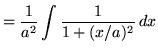 .
.
Now let
u= x/a
so that
du = (1/a) dx ,
or
(a)du = dx .
Now substitute into the original problem, replacing all forms of x, and getting
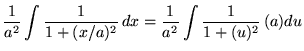
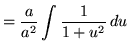
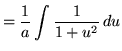
![]()
![]() .
.
We now have the following variation of formula 1 :
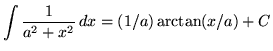
Recall also the method of algebraically "completing the square". For example to complete the square with x2+6x we divide 6 by 2, square it getting 9, add and subtract 9, so that
x2+6x = (x2+6x+9) - 9 = (x+3)2 - 9 .
To complete the square with x2+Bx , divide B by 2, square it getting (B/2)2=B2/4, add and subtract B2/4, so that
x2+Bx = (x2+Bx+B2/4) - B2/4 = (x+(B/2))2 - B2/4 .
As you do the following problems, remember these three general rules for integration :
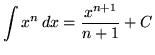 ,
,
where n is any constant not equal to -1,
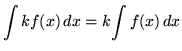 ,
,
where k is any constant, and
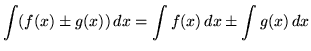 .
.
Most of the following problems are average. A few are challenging. Knowledge of the method of u-substitution will be required on many of the problems. Make precise use of the differential notation dx and du and always be careful when arithmetically and algebraically simplifying expressions. There is a very high emphasis on arithmetic and algebra in this problem set. AVOID MAKING THE FOLLOWING VERY COMMON ALGEBRA MISTAKE :
THIS IS FALSE :
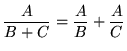 .
.
Convince yourself that this is generally INCORRECT by plugging numbers in for A, B, and C (Try A=4, B=2, and C=2 .).
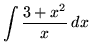 .
.
Click HERE to see a detailed solution to problem 1.
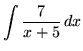 .
.
Click HERE to see a detailed solution to problem 2.
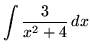 .
.
Click HERE to see a detailed solution to problem 3.
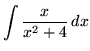 .
.
Click HERE to see a detailed solution to problem 4.
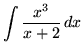 .
.
Click HERE to see a detailed solution to problem 5.
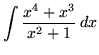 .
.
Click HERE to see a detailed solution to problem 6.
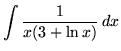 .
.
Click HERE to see a detailed solution to problem 7.
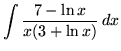 .
.
Click HERE to see a detailed solution to problem 8.
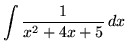 .
.
Click HERE to see a detailed solution to problem 9.
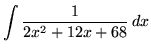 .
.
Click HERE to see a detailed solution to problem 10.
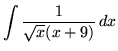 .
.
Click HERE to see a detailed solution to problem 11.
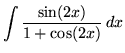 .
.
Click HERE to see a detailed solution to problem 12.
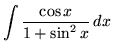 .
.
Click HERE to see a detailed solution to problem 13.
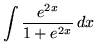 .
.
Click HERE to see a detailed solution to problem 14.
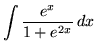 .
.
Click HERE to see a detailed solution to problem 15.
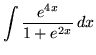 .
.
Click HERE to see a detailed solution to problem 16.
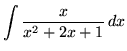 .
.
Click HERE to see a detailed solution to problem 17.
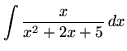 .
.
Click HERE to see a detailed solution to problem 18.
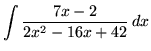 .
.
Click HERE to see a detailed solution to problem 19.
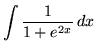 .
.
Click HERE to see a detailed solution to problem 20.
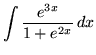 .
.
Click HERE to see a detailed solution to problem 21.
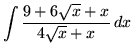 .
.
Click HERE to see a detailed solution to problem 22.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :