Shell Method Solution 1

Processing math: 100%

Solution 9.): Here is a carefully labeled sketch of the circle with a shell marked on the

$x$ -axis at

$x$ . The shell has radius

$r$ , measured from the line

$x=-b$ -axis, and height

$h$ , taken parallel to the

$y$ -axis at

$x$ . It is IMPORTANT to mark ALL

$x$ ,

$r$ , and

$h$ in the sketch of the region !!!

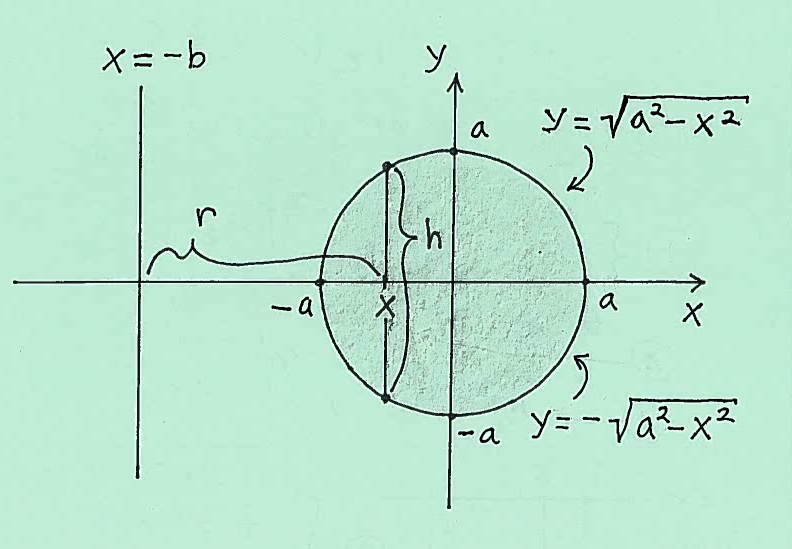
tex2html_wrap_inline125

Thus the total volume of this Solid of Revolutions is

$Volume = 2 \pi \int_{-a}^{a} (radius)(height) \ dx = 2 \pi \int_{-a}^{a} rh \ dx$

$= 2 \pi \int_{-a}^{a} (x-(-b))(\sqrt{a^2-x^2} - (- \sqrt{a^2-x^2} \ )) \ dx$

$= 2 \pi \int_{-a}^{a} (x+b) (2 \cdot \sqrt{a^2-x^2} \ ) \ dx$

$= 2 \pi \int_{-a}^{a} 2x \cdot \sqrt{a^2-x^2} \ dx \ \ + \ \ 2 \pi \int_{-a}^{a} 2b \cdot \sqrt{a^2-x^2} \ dx$

$= 4 \pi \int_{-a}^{a} x \cdot \sqrt{a^2-x^2} \ dx \ \ + \ \ 4b \pi \int_{-a}^{a} \cdot \sqrt{a^2-x^2} \ dx$ (Use a standard u-substitution for the first integral. Use the fact that the second integral is the area of the top semi-circle.)

$= 4 \pi \cdot {-1 \over 2} {2 \over 3} (a^2-x^2)^{3/2} \Big|_{-a}^{a} \ \ + \ \ 4b \pi \cdot {1 \over 2} \pi a^2$

$= {-4 \over 3} \pi ( (a^2-(a)^2)^{3/2} - (a^2-(-a)^2)^{3/2} ) \ \ + \ \ 2 \pi^2 a^2 b$

$= {-4 \over 3} \pi ( 0 - 0 ) \ \ + \ \ 2 \pi^2 a^2 b$ i.e.,

$Volume = 2 \pi^2 a^2 b$

Click HERE to return to the list of problems.