SOLUTION 7: $ \ \ $ To integrate $ \displaystyle{ \int {
\sqrt{x^2-9} \over x^2 } \ dx } $ use the trig substitution
$$ x = 3 \sec \theta $$
so that
$$ dx = 3 \sec \theta \tan \theta \ d \theta $$
Substitute into the original problem, replacing all
forms of x, getting
$$ \displaystyle { \int \frac{\sqrt{x^{2}-9}}{x^{2}} \ dx = \int
\frac{\sqrt{9 \sec^{2} \theta - 9}}{9 \sec^{2} \theta} \cdot 3
\sec \theta \tan \theta \ d \theta } $$
$$ = \displaystyle { \int \frac{\sqrt{9 (\sec^{2} \theta - 1 )}}{9 \sec^{2} \theta} \cdot 3
\sec \theta \tan \theta \ d \theta } $$
$$ = \displaystyle { \int \frac{\sqrt{9 \tan^{2} \theta}}{9
\sec^{2} \theta} \cdot 3 \sec \theta \tan \theta \ d \theta } $$
$$ = \displaystyle { \int \frac{3 \tan \theta}{9 \sec^{2} \theta}
\cdot 3 \sec \theta \tan \theta \ d \theta } $$
$$ = \displaystyle { \int \frac{\tan^{2} \theta}{\sec \theta} \ d
\theta } $$
$$ = \displaystyle { \int \frac{\sec^{2} \theta - 1}{\sec \theta} \
d \theta} $$
$$ = \displaystyle { \int \Big( \frac{ \sec^2 \theta}{ \sec \theta } - \frac{1}{\sec \theta}) \ d
\theta } $$
$$ = \displaystyle { \int (\sec \theta - \cos \theta) \ d \theta } $$
(Recall that $ \displaystyle { \int \sec \theta \ d
\theta = \ln \Big|\sec \theta + \tan \theta \Big| + C } . $)
$$ = \displaystyle { \ln \Big|\sec \theta + \tan \theta \Big| - \sin \theta
+ C } $$
$ \Big( $We need to write our final answer in terms of $x$.
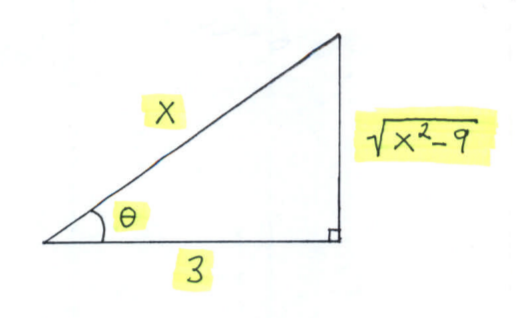
Since $ x = 3 \sec \theta $ it follows that
$$ \sec \theta = \displaystyle{ x \over 3 } = \displaystyle{ hypotenuse \over adjacent } $$
and from the Pythagorean Theorem that
$$ \displaystyle (adjacent)^2 + (opposite)^2 = (hypotenuse)^2
\ \ \longrightarrow $$
$$ (3)^2 + (opposite)^2 = (x)^2
\ \ \longrightarrow \ \ \ opposite = \sqrt{x^2-9} \ \ \longrightarrow $$
$$ \sin \theta = \displaystyle{ opposite \over hypotenuse }= \displaystyle{ \sqrt{x^2-9} \over x } $$
and
$$ \tan \theta = \displaystyle{ opposite \over adjacent }= \displaystyle{ \sqrt{x^2-9} \over 3 } . \Big) $$
$$ = \displaystyle { \ln \Big|\frac{x}{3} + \frac{\sqrt{x^{2}-9}}{3} \Big| -
\frac{\sqrt{x^{2}-9}}{x} + C } $$
Click HERE to return to the list of problems.

