Trig Sub Solution 11

Processing math: 100%

SOLUTION 11:

$\ \$ To integrate

$\displaystyle{ \int { x \over \sqrt{x^4-16} } \ dx = \int { x \over \sqrt{(x^2)^2-16} } \ dx }$ begin with the ordinary u-substitution

$u = x ^{2}$ so that

$du = 2x \ dx$ Substitute into the original problem, replacing all forms of x, getting

$\displaystyle { \int \frac{x}{\sqrt{x^{4}-16}} \ dx = \int \frac{1/2}{\sqrt{u^{2}-16}} \ du }$ Now use the trig substitution

$u = 4 \sec \theta$ so that

$du = 4 \sec \theta \tan \theta \ d \theta$ Substitute into the original problem, replacing all forms of u, getting

$= \displaystyle { \int \frac{1/2}{\sqrt{(4 \sec \theta )^{2}-16}} \ du }$

$= \displaystyle { \int \frac{1/2}{\sqrt{16 \sec^{2} \theta - 16}} \cdot 4 \sec \theta \tan \theta \ d \theta }$

$= \displaystyle { \int \frac{1/2}{\sqrt{16 ( \sec^{2} \theta - 1)}} \cdot 4 \sec \theta \tan \theta \ d \theta }$

$= \displaystyle { 2 \int \frac{\sec \theta \tan \theta}{\sqrt{16 \tan^{2} \theta}} \ d \theta }$

$= \displaystyle { 2 \int \frac{\sec \theta \tan \theta}{4 \tan \theta} \ d \theta }$

$= \displaystyle { \frac{1}{2} \int \sec \theta \ d \theta }$

$= \displaystyle { \frac{1}{2} (\ln \Big|\sec \theta + \tan \theta \Big| + C) }$

$\Big($ We need to write our final answer in terms of

$x$ .

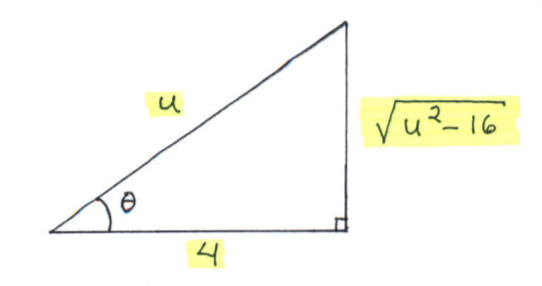
tex2html_wrap_inline125

Since

$u = 4 \sec \theta$ it follows that

$\sec \theta = \displaystyle{ u \over 4 } = \displaystyle{ hypotenuse \over adjacent }$ and from the Pythagorean Theorem that

$\displaystyle (adjacent)^2 + (opposite)^2 = (hypotenuse)^2 \ \ \longrightarrow$

$(4)^2 + (opposite)^2 = (u)^2 \ \ \longrightarrow \ \ \ opposite = \sqrt{u^2-16} \ \ \longrightarrow$

$\tan \theta = \displaystyle{ opposite \over adjacent }= \displaystyle{ \sqrt{u^2-16} \over 4 } . \Big)$

$= \displaystyle { \frac{1}{2} (\ln \Big|{ u \over 4 } + { \sqrt{u^2-16} \over 4 }\Big| + C) }$ (Now use the fact that

$u=x^2$ .)

$= \displaystyle { \frac{1}{2} (\ln \Big|\frac{x^{2}}{4} + \frac{\sqrt{x^{4}-16}}{4} \Big| + C) }$

Click HERE to return to the list of problems.