COMPUTING THE VOLUME OF STATIC SOLIDS USING CROSS-SECTIONAL AREA
The following problems involve the use of integrals to compute the volume of static solids using cross-sectional area. Imagine a solid suspended above the $x$-axis from $ x=a $ to $ x=b $. We will assume that the cross-sectional of the solid taken perpendicular to the $x$-axis at $x$ is known to be $ A(x) $. Now consider a thin slice of this solid at $x$ of thickness $ dx $.
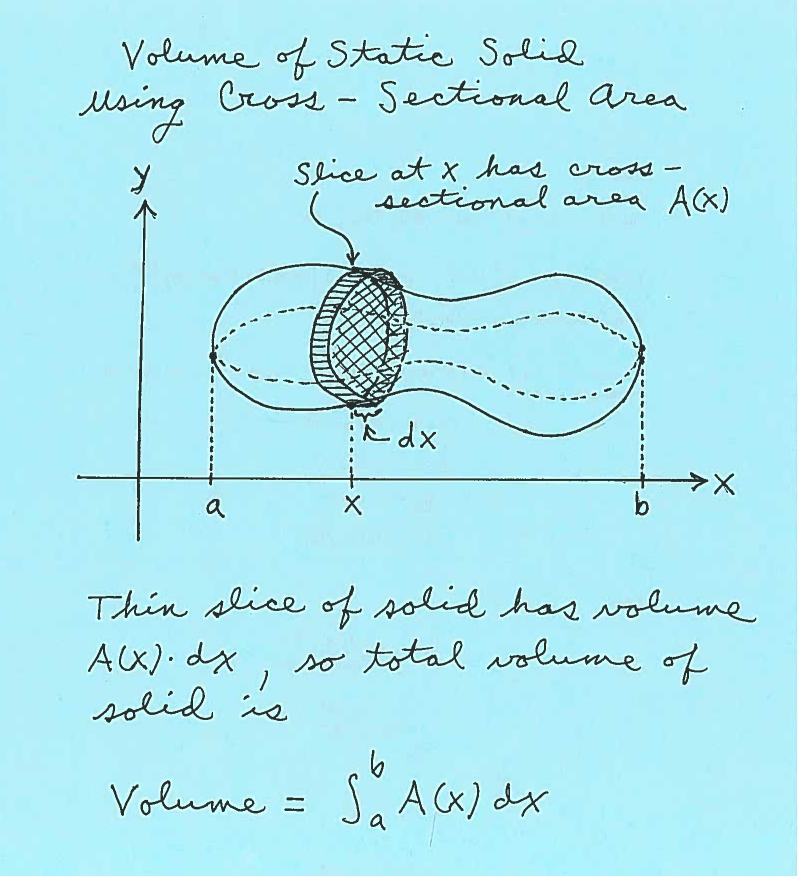
After carefully reading the description of a static solid and drawing some appropriate sketches, it will be our job to create a function of $x$, $ a \le x \le b $, which represents the area $A(x)$ of a cross-sectional slice at $x$. Then the total volume of the static solid will be
$$ Volume = \int_{a}^{b} A(x) \ dx $$
EXAMPLE 1: The flat base of a solid sits in the $xy$-plane in the region bounded by the graphs of $ y=0 $ and $ y=e^{-x} $ between $ x=0 $ and $ x=4 $. SET UP but do not evaluate an integral which represents the volume of this solid if cross-sections take perpendicular to the $x$-axis at $x$ are squares. (See the graphs below.).
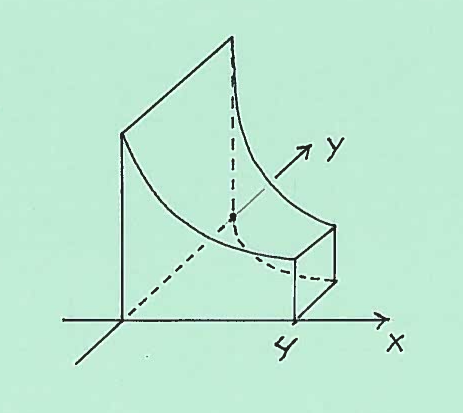
Here are sketches of the base of the solid and the entire solid.
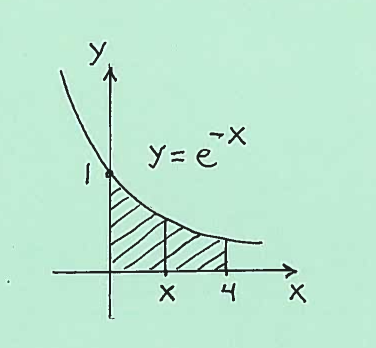 $ \ \ \ $
$ \ \ \ $
Here are sketches of a square cross-section at $x$ together with its dimensions.
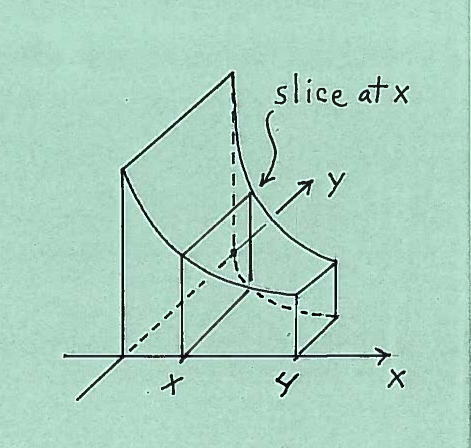 $ \ \ \ $
$ \ \ \ $
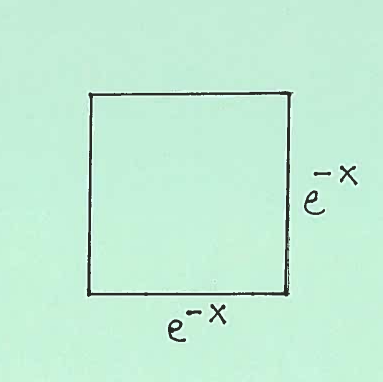
The area of the square cross-section is $ A(x)= (edge)^2 = (e^{-x})^2 $. Thus the total volume of this static solid is
$$ Volume = \int_{0}^{4} (e^{-x})^2 \ dx $$
The following problems use integration to find the volume of static solids using cross-sectional area. Most are average. A few are somewhat challenging. All solutions SET UP the integrals but do not evaluate them. We leave the actual integration of the integrals up to you, using antiderivatives or online integrators.
- PROBLEM 1 : The flat base of a solid sits in the $xy$-plane in the region bounded by the $x$-axis, the $y$-axis, and the line $ x+2y=6 $. SET UP but do not evaluate an integral which represents the volume of this solid if cross-sections take perpendicular to the $x$-axis at $x$ are
$ \ \ \ \ $ a.) squares.
$ \ \ \ \ $ b.) semi-circles.
$ \ \ \ \ $ c.) rectangles of height 5.
Click HERE to see a detailed solution to problem 1.
- PROBLEM 2 : The flat base of a solid sits in the $xy$-plane in the region bounded by the $x$-axis, the line $x=e^2$, and $ y= \ln x $. SET UP but do not evaluate an integral which represents the volume of this solid if cross-sections take perpendicular to the $x$-axis at $x$ are
$ \ \ \ \ $ a.) squares.
$ \ \ \ \ $ b.) quarter-circles.
$ \ \ \ \ $ c.) isosceles triangles of height 4.
Click HERE to see a detailed solution to problem 2.
- PROBLEM 3 : The flat base of a solid sits in the $xy$-plane in the region bounded by the $x$-axis, the line $y=8$, and $ y=x^3 $. SET UP but do not evaluate an integral which represents the volume of this solid if cross-sections take perpendicular to the $x$-axis at $x$ are
$ \ \ \ \ $ a.) squares.
$ \ \ \ \ $ b.) equilateral triangles.
$ \ \ \ \ $ c.) rectangles of perimeter 16.
Click HERE to see a detailed solution to problem 3.
Click HERE to return to the original list of various types of calculus problems.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by
clicking on the following address :
kouba@math.ucdavis.edu
A heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easy.
Duane Kouba ...
October 7, 2020


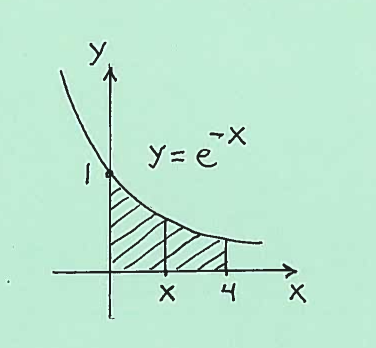 $ \ \ \ $
$ \ \ \ $

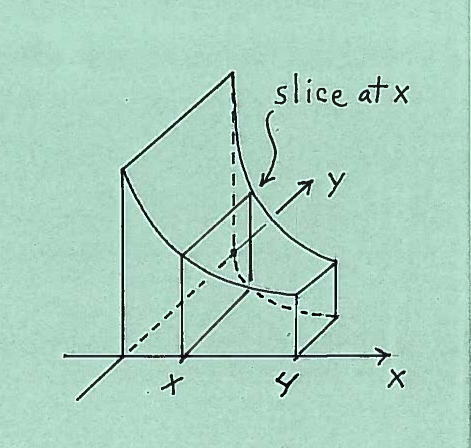 $ \ \ \ $
$ \ \ \ $
