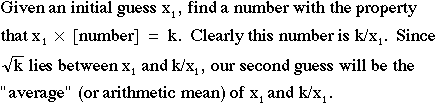
Square Roots Revisited

Having implemented the Babylonian method for finding the square root of 2, we can reformulate the underlying idea for a general number k.

Finding the square root of k is a search for a number n with the property that n x n = k. What the Babylonians discovered is an iterative method for taking an initial guess and then improving on it.

The Babylonian method of "divide and average" can be formulated as follows:

In other words,

More generally, the Babylonian method for finding (or approximating) the square root of k can be summarized by 

Exercise. Suppose someone makes an initial guess to the effect that "the square root of 5 is 2." Use the Babylonian method to determine the second guess of 9/4. Use a hand calculator to confirm that the third guess is correct up to the fourth decimal place.

Proceed to the NEXT PAGE Return to the PRECEDING PAGE