SOLUTION 15: Consider the graphs of $y=f(x)$ and $y=x$ on the interval $ [0, 1]$ with $ f(0)>0 $ and $ f(1)<1 $.
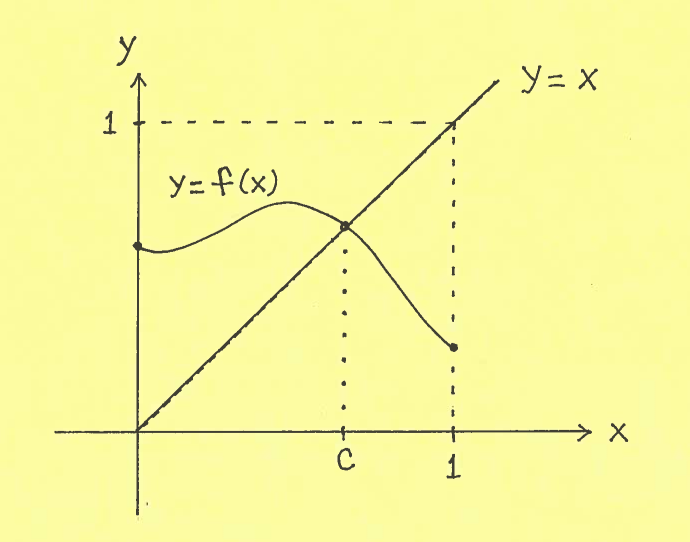
Let function
$$ g(x)= f(x)-x \ \ \ \ and \ choose \ \ \ \ m=0 $$
Function $g$ is continuous on the interval $ [0, 1] $ since it is the DIFFERENCE of continuous functions. Note that
$$ g(0) = f(0) - 0 = f(0)>0 $$
and
$$ g(1)=f(1) - 1 < 0 $$
i.e., $m=0$ is between $ f(0) $ and $ f(1) $.
The assumptions of the Intermediate Value Theorem have now been met on the interval $[0, 1]$, so we can conclude that there is some number $c$ in the interval $[0, 1]$ which satisfies
$$ g(c)=m $$
i.e.,
$$ f(c)-c =0 \ \ \ \ \longrightarrow \ \ \ \ f(c)=c $$
This completes the proof.
Click HERE to return to the list of problems.

