![]()
![]()
(Factor an x from each term.)
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 2 : Differentiate ![]() . Apply the quotient rule. Then
. Apply the quotient rule. Then
![]()
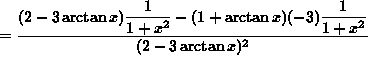
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 3 : Differentiate ![]() arc
arc![]() arc
arc![]() .
Apply the product rule. Then
.
Apply the product rule. Then
![]() arc
arc![]() arc
arc![]() arc
arc![]() arc
arc![]()
![]() arc
arc![]() arc
arc![]()
= ( arc![]() arc
arc![]() .
.
Click HERE to return to the list of problems.
SOLUTION 4 : Let ![]() arc
arc![]() . Solve f'(x) = 0 for x . Begin by differentiating f . Then
. Solve f'(x) = 0 for x . Begin by differentiating f . Then
![]()
![]()
(Get a common denominator and subtract fractions.)
![]()
![]()
![]()
![]()
![]() .
.
(It is a fact that if ![]() , then A = 0 .) Thus,
, then A = 0 .) Thus,
2(x - 2)(x+2) = 0 .
(It is a fact that if AB = 0 , then A = 0 or B=0 .) It follows that
x-2 = 0 or x+2 = 0 ,
that is, the only solutions to f'(x) = 0 are
x = 2 or x = -2 .
Click HERE to return to the list of problems.
SOLUTION 5 : Let ![]() . Show that f'(x) = 0 . Conclude that
. Show that f'(x) = 0 . Conclude that
![]() . Begin by differentiating f . Then
. Begin by differentiating f . Then
![]() .
.
If f'(x) = 0 for all admissable values of x , then f must be a constant function, i.e.,
![]() for all admissable values of x ,
for all admissable values of x ,
i.e.,
![]() for all admissable values of x .
for all admissable values of x .
In particular, if x = 0 , then
![]()
i.e.,
![]() .
.
Thus, ![]() and
and ![]() for all admissable values of x .
for all admissable values of x .
Click HERE to return to the list of problems.
SOLUTION 6 : Evaluate 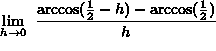 . It may not be obvious, but this problem can be viewed as a derivative problem. Recall that
. It may not be obvious, but this problem can be viewed as a derivative problem. Recall that
![]()
(Since h approaches 0 from either side of 0, h can be either a positve or a negative number. In addition,
![]() is equivalent to
is equivalent to ![]() . This explains the following
equivalent variations in the limit definition of the derivative.)
. This explains the following
equivalent variations in the limit definition of the derivative.)
![]()
![]() .
.
If ![]() , then
, then ![]() , and letting
, and letting
![]() , it follows that
, it follows that
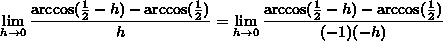
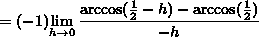
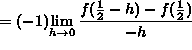
![]()
![]()
![]()
![]()
![]()
![]() .
.
The following problems require use of the chain rule.
Click HERE to return to the list of problems.
SOLUTION 7 : Differentiate ![]() . Use the product rule first. Then
. Use the product rule first. Then
![]()
(Apply the chain rule in the first summand.)
![]()
![]()
(Factor out ![]() . Then get a common denominator and add.)
. Then get a common denominator and add.)
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 8 : Differentiate ![]() . Apply the chain rule twice. Then
. Apply the chain rule twice. Then
![]()
![]()
(Recall that ![]() .)
.)
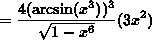
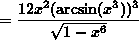 .
.
Click HERE to return to the list of problems.
SOLUTION 9 : Differentiate ![]() . Apply the chain rule twice. Then
. Apply the chain rule twice. Then
![]()
(Recall that ![]() .)
.)
![]()
![]()
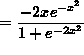 .
.
Click HERE to return to the list of problems.
SOLUTION 10 : Determine the equation of the line tangent to the graph of ![]() at x = e . If x = e , then
at x = e . If x = e , then ![]() , so that the line passes through the point
, so that the line passes through the point ![]() . The slope of the tangent line follows from the derivative (Apply the chain rule.)
. The slope of the tangent line follows from the derivative (Apply the chain rule.)
![]()
![]()
![]() .
.
The slope of the line tangent to the graph at x = e is
![]()
![]()
![]() .
.
Thus, an equation of the tangent line is
![]() .
.
Click HERE to return to the list of problems.