Related Rates Solution 1

Processing math: 100%

SOLUTION 1: Draw a square with edges labeled

$x$ , and assume each edge is a function of time

$t$ .

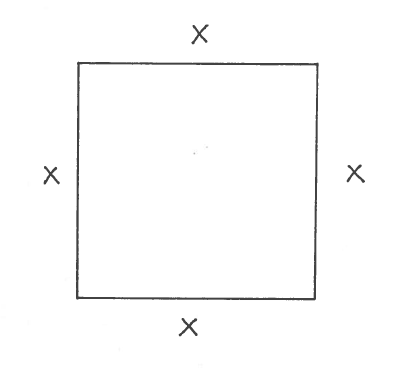
tex2html_wrap_inline125

$\ \ \ \$ a.) The perimeter of the square is

$P=x+x+x+x \ \ \ \ \longrightarrow$

$P=4x$ GIVEN:

$\ \ \ \displaystyle{ dx \over dt } = 3 \ cm/sec.$

FIND:

$\ \ \ \displaystyle{ dP \over dt }$ when

$x=10 \ cm.$

Now differentiate the perimeter equation with repect to time

$t$ , getting

$D \{ P \} = D \{4x\} \ \ \ \longrightarrow$

$\displaystyle{ dP \over dt } = 4 \displaystyle{ dx \over dt } \ \ \ \longrightarrow$

$\Big($ Now let

$\displaystyle{ dx \over dt } = 3. \Big)$

$\displaystyle{ dP \over dt } = 4 (3) = 12 \ cm/sec.$

$\ \ \ \$ b.) The area of the square is

$A=(base)(height)= x \cdot x \ \ \ \ \longrightarrow$

$A=x^2$ GIVEN:

$\ \ \ \displaystyle{ dx \over dt } = 3 \ cm/sec.$

FIND:

$\ \ \ \displaystyle{ dA \over dt }$ when

$x=10 \ cm.$

Now differentiate the area equation with respect to time

$t$ , getting

$D \{ A \} = D \{x^2 \} \ \ \ \longrightarrow$

$\displaystyle{ dA \over dt } = 2x \displaystyle{ dx \over dt } \ \ \ \longrightarrow$

$\Big($ Now let

$\displaystyle{ dx \over dt } = 3$ and

$x=10. \Big)$

$\displaystyle{ dA \over dt } = 2 (10) (3) = 60 \ cm^2/sec.$

Click HERE to return to the list of problems.