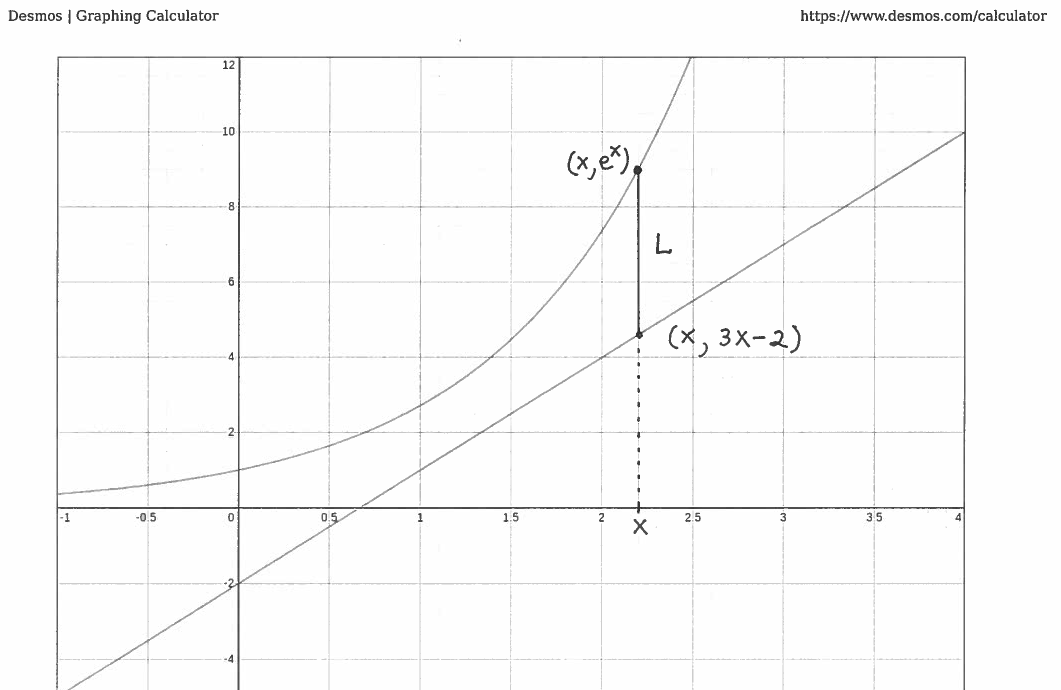
SOLUTION 18: Since $ \displaystyle{ dx \over dt } = 1 \ mile/min. $ and the cars start at $x=0$, it follows that $x=t$ determines the $x$-value at time $t$ minutes for each car. Let $L$ be the distance between the cars after $t$ minutes and assume that $x$ and $L$ are both functions of time $t$ minutes.
GIVEN: $ \ \ \ \displaystyle{ dx \over dt } = 1 \ mile/min. $
FIND: $ \ \ \ \displaystyle{ dL \over dt } $ when $ \ \ $ a.) $ \ t=1 \ min. $ $ \ \ $ b.) $ \ t=3 \ min. $
The distance between the two cars after $t$ minutes is
$$ L = e^x-(3x-2) \ \ \ \ \longrightarrow $$
$$ L = e^x-3x+2 $$
Differentiating this distance equation, we get
$$ D \{ L \} = D \{ \displaystyle{ e^x-3x+2 } \} \ \ \ \ \longrightarrow $$
$\Big($Recall that $ D \{ e^{f(t)} \} = e^{f(t)} \cdot f'(t).\Big) $
$$ (**) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \displaystyle{ dL \over dt } = e^x \cdot \displaystyle{ dx \over dt } - 3 { dx \over dt } \ \ \ \ \longrightarrow $$
$\Big( $a.) Now let $ \displaystyle{ dx \over dt } = 1 $ and $ \ t=1 $, so that $ \ x=1 $ in equation (**).$\Big)$
$$ \displaystyle{ dL \over dt } = e^{1}(1) - 3 (1) \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dL \over dt } = e-3 \approx -0.282 \ miles/min. $$
$\Big($ b.) Now let $ \displaystyle{ dx \over dt } = 1 $ and $ \ t=3 $, so that $ \ x=3 $ in equation (**).$\Big)$
$$ \displaystyle{ dL \over dt } = e^{3}(1) - 3 (1) \ \ \ \ \longrightarrow $$
$$ \displaystyle{ dL \over dt } = e^3-3 \approx 17.086 \ miles/min. $$
Click HERE to return to the list of problems.

