Area Solution 6

Processing math: 100%

SOLUTION 6: Compute the area of the region enclosed by the graphs of the equations

$y=\ln x$ ,

$y=1$ and

$x=e^{2}$ . Begin by finding the points of intersection of the two graphs. From

$y=\ln x$ and

$y=1$ we get that

$\ln x = 1 \ \ \longrightarrow \ \ \ x=e$ Now see the given graph of the enclosed region.

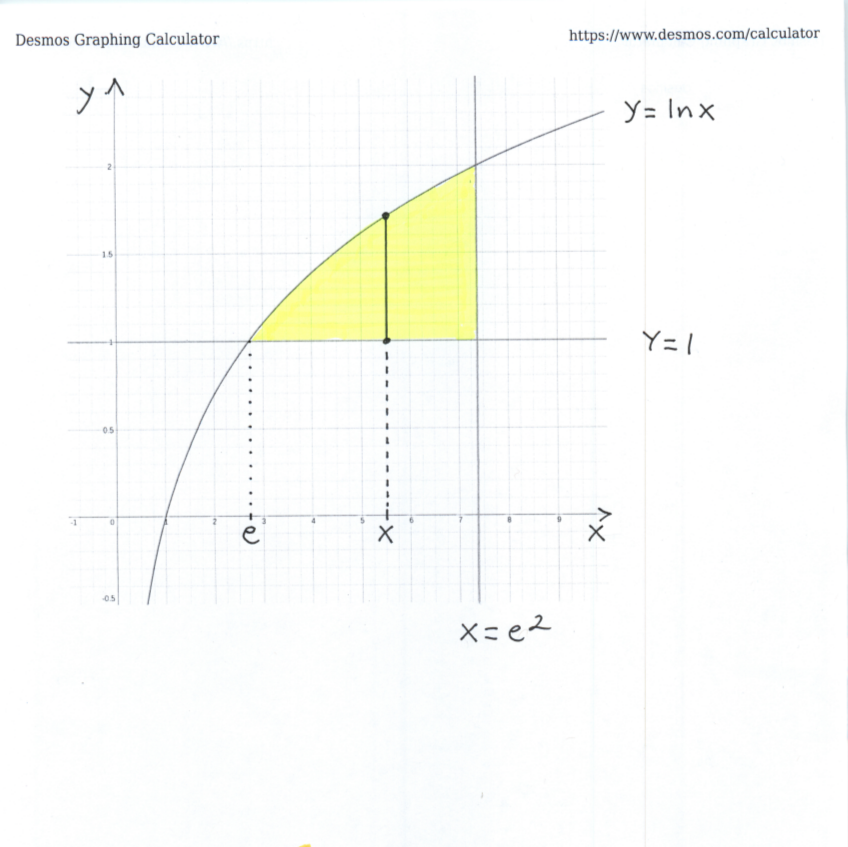
tex2html_wrap_inline125

Using vertical cross-sections to describe this region, we get that

$e \le x \le e^2 \ \ and \ \ 1 \le y \le \ln x ,$ so that the area of this region is

$AREA = \displaystyle{ \int_{e}^{e^{2}} (Top \ - \ Bottom) \ dx }$

$= \displaystyle { \int_{e}^{e^{2}} (\ln x - 1) \ dx }$

$= \displaystyle { \int_{e}^{e^{2}} \ln x \ dx - \int_{e}^{e^{2}} 1 \ dx }$

$\Big($ For

$\displaystyle { \int \ln x \ dx } \$ use Integration by Parts. Recall that the Integration by Parts Formula is

$\ \displaystyle { \int u \ dv = uv - \int v \ du }$ . Let

$\ u = \ln x \$ and

$\ dv = dx \$ , so that

$\ du = \displaystyle{ 1 \over x } \ dx \$ and

$\ v = x \$ . Then

$\displaystyle{ \int \ln x \ dx } = \displaystyle { x \ln x - \int \Big(\frac{1}{x}\Big)(x) \ dx } = \displaystyle { x \ln x - \int 1 \ dx } = \displaystyle { x \ln x - x + C } . \Big)$

$= \displaystyle { \Big( (x \ln x - x) - x \Big) \Big\vert_{e}^{e^{2}} }$

$= \displaystyle { \Big( x \ln x - 2x \Big) \Big\vert_{e}^{e^{2}} }$

$= \displaystyle { \Big( e^{2} \ln e^{2} - 2e^{2} \Big) - \Big( e \ln e - 2e \Big) }$

$= \displaystyle { \Big( e^{2}(2) - 2e^{2} \Big) - \Big( e(1) - 2e \Big) }$

$= \displaystyle { \Big( 0 \Big) - \Big( -e \Big) }$

$= \displaystyle { e }$

Click HERE to return to the list of problems.