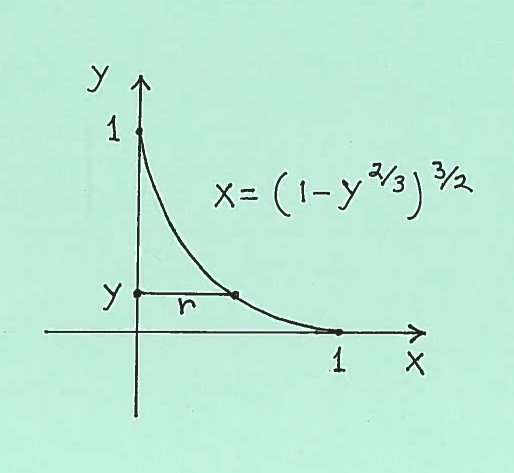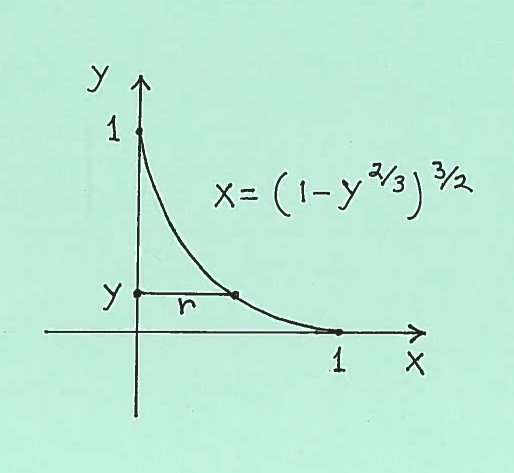Solution 9: First solve the equation $ x^{2/3} + y^{2/3}=1$ for $x$ getting
$$ x^{2/3} = 1 - y^{2/3} \ \ \ \longrightarrow $$
$$ x = (1 - y^{2/3})^{3/2} $$
Here is a carefully labeled sketch of the graph with a radius $r$ marked together with $y$ on the $y$-axis. We will find the surface area of the TOP HALF of theSurface of Revolution and DOUBLE our answer.
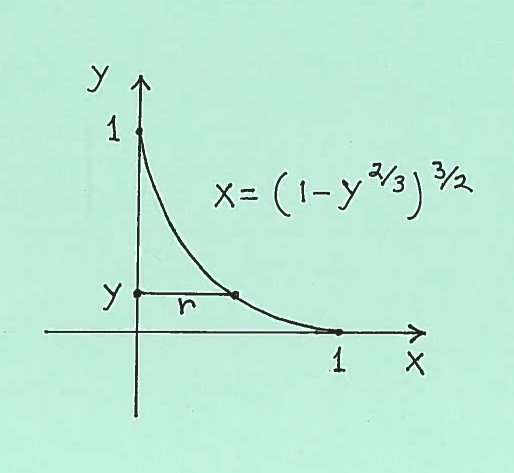
The derivative of $x$ is
$$ { dx \over dy } = {3 \over 2} (1-y^{2/3})^{1/2} \cdot {-2 \over 3}y^{-1/3} \ \ \ \longrightarrow $$
$$ { dx \over dy } = { -(1-y^{2/3})^{1/2} \over y^{1/3} } $$
Thus the total Area of this Surface of Revolution is
$$ Surface \ Area = 2 \pi \cdot 2 \int_{0}^{1} (radius) \sqrt{ 1 + \Big({dx \over dy}\Big)^2 } \ dy $$
$$ = 4 \pi \int_{0}^{1} (1-y^{2/3})^{3/2} \sqrt{ 1 + \Big( {-(1-y^{2/3})^{1/2} \over y^{1/3}} \Big)^2 } \ dy $$
$$ = 4 \pi \int_{0}^{1} (1-y^{2/3})^{3/2} \sqrt{ 1 + { {1-y^{2/3}} \over y^{2/3}} } \ dy $$
$$ = 4 \pi \int_{0}^{1} (1-y^{2/3})^{3/2} \sqrt{ { {y^{2/3} + (1-y^{2/3}) } \over y^{2/3}} } \ dy $$
$$ = 4 \pi \int_{0}^{1} (1-y^{2/3})^{3/2} \sqrt{ { 1 \over y^{2/3} } } \ dy $$
$$ = 4 \pi \int_{0}^{1} (1-y^{2/3})^{3/2} \cdot { 1 \over y^{1/3} } \ dy $$
$$ = 4 \pi \int_{0}^{1} { (1-y^{2/3})^{3/2} \over y^{1/3} } \ dy $$
$\Big($ Let's do a $u$-substitution. Let $ u= 1-y^{2/3} \ $ so that $ \ du = (-2/3)y^{-1/3} dy \ \ \longrightarrow \ \ (-3/2) du = {1 \over y^{1/3}} dy.\ \ $ Since $ \ y:0 \rightarrow 1 \ $ and $ \ u= 1-y^{2/3} \ $, it follows that $ \ u:1 \rightarrow 0. \ $ Now make the substitutions. $\Big)$
$$ = 4 \pi \int_{1}^{0} u^{3/2} \ (-3/2) du $$
$$ = 4 \pi (-3/2) \int_{1}^{0} u^{3/2} \ du $$
$$ = -6 \pi \cdot (2/5)u^{5/2} \Big|_{1}^{0} $$
$$ = -6 \pi \Big( (2/5)(0)^{5/2} - (2/5)(1)^{5/2} \Big) $$
$$ = -6 \pi ( 0 - 2/5 ) $$
$$ = (12/5) \pi $$
Click HERE to return to the list of problems.