Next: About this document ...
truein truein Math 16A
Kouba
The Derivative of Sin x
truein truein truein truein truein
FACTS: 1.)
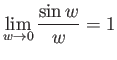 truein
2.)
truein
2.)
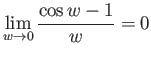 truein
3.)
truein
3.)
![]()
truein
truein
truein
Let ![]() .
Then
.
Then
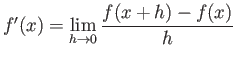
truein truein
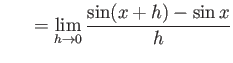
truein truein
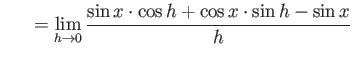
truein truein
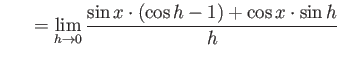
truein truein
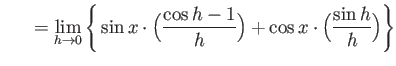
truein truein
![]()
truein truein
![]()