Next: About this document ...
PROBLEM 1: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() ,
, ![]() , and
, and ![]() .
.
trueintruein
SOLUTION 1: Compute the area of the enclosed
region bounded by the graphs of the equations ![]() ,
, ![]() and
and ![]() . Begin by finding the points of intersection of the
two graphs. From
. Begin by finding the points of intersection of the
two graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
Using vertical cross-sections we get that
truein
AREA
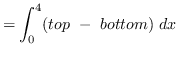
truein
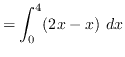
truein
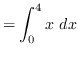
truein
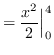
truein
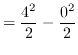
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 2: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() and
and ![]() .
.
trueintruein
SOLUTION 2: Compute the area of the enclosed
region bounded by the graphs of the equations ![]() and
and ![]() . Begin by finding the points of intersection of the two
graphs. From
. Begin by finding the points of intersection of the two
graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
![]() or
or ![]()
truein
Using vertical cross-sections we get that
truein
AREA
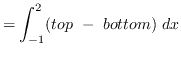
truein
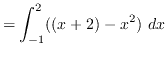
truein
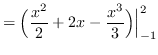
truein
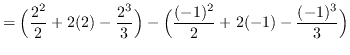
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]() .
.
trueintrueintruein
PROBLEM 3: Compute the area of the enclosed region
bounded by the graphs of the equations
![]() and
and
![]() .
.
trueintruein
SOLUTION 3: Compute the area of the enclosed
region bounded by the graphs of the equations ![]() ,
, ![]() , and
, and ![]() . Begin by finding the points of
intersection of the two graphs. From
. Begin by finding the points of
intersection of the two graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
Using vertical cross-sections we get that
truein
AREA
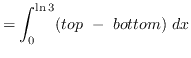
truein
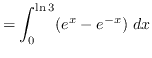
truein
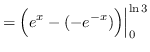
truein
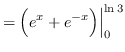
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 4: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() and
and ![]() .
.
trueintruein
SOLUTION 4: Compute the area of the enclosed
region bounded by the graphs of the equations ![]() and
and ![]() . Begin by finding the points of intersection of
the two graphs. From
. Begin by finding the points of intersection of
the two graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]() or
or ![]()
truein
Using vertical cross-sections we get that
truein
AREA
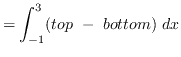
truein
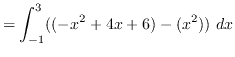
truein
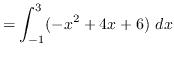
truein
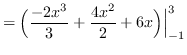
truein
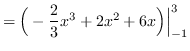
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 5: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() and
and ![]() .
.
trueintruein
SOLUTION 2: Compute the area of the enclosed
region bounded by the graphs of the equations ![]() and
and ![]() . Begin by finding the points of intersection of the
two graphs. From
. Begin by finding the points of intersection of the
two graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]() ,
, ![]() , or
, or ![]()
truein
Using vertical cross-sections we get that
truein
AREA
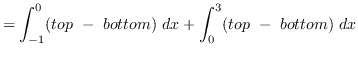
truein
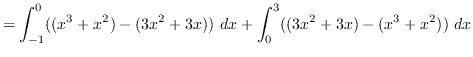
truein
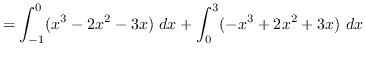
truein
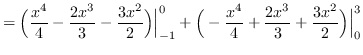
truein
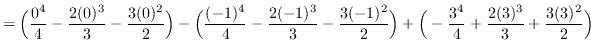
truein
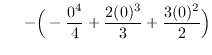
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 6: Compute the area of the enclosed region
bounded by the graphs of the equations
![]() and
and ![]() .
.
trueintruein
SOLUTION 6: Compute the area of the enclosed
region bounded by the graphs of the equations ![]() ,
, ![]() and
and ![]() . Begin by finding the points of intersection of
the two graphs. From
. Begin by finding the points of intersection of
the two graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
Using vertical cross-sections we get that
truein
AREA
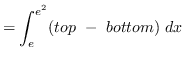
truein
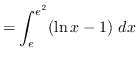
truein
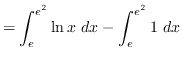
truein
Let
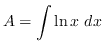 .
.
truein
Use integration by parts. Let ![]() and
and ![]() such that
such that
![]() and
and ![]() .
.
truein
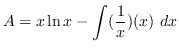
truein
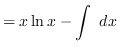
truein
![]()
truein
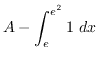
truein
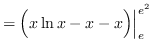
truein
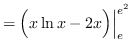
truein
![]()
truein
![]()
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 7: Compute the area of the enclosed region
bounded by the graphs of the equations
![]() and
and ![]() .
.
trueintruein
SOLUTION 7: Compute the area of the enclosed
region bounded by the graphs of the equations ![]() ,
, ![]() and
and ![]() . Begin by finding the points of
intersection of the two graphs. From
. Begin by finding the points of
intersection of the two graphs. From ![]() and
and ![]() we
get that
we
get that
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
Using vertical cross-sections we get that
truein
AREA
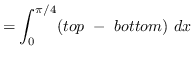
truein
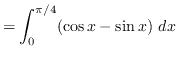
truein
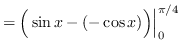
truein
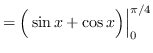
truein
![]()
truein
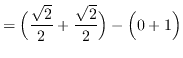
truein
![]()
trueintrueintruein
PROBLEM 8: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() and
and ![]() .
.
trueintruein
SOLUTION 8: Compute the area of the enclosed
region bounded by the graphs of the equations
![]() ,
,
![]() and
and ![]() . Begin by finding the points of
intersection of the two graphs. From
. Begin by finding the points of
intersection of the two graphs. From
![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
![]() or
or
![]()
truein
![]() or
or ![]()
truein
Using horizontal cross-sections such that
![]() and
and
![]() we get that
we get that
truein
AREA
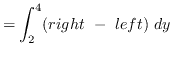
truein
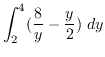
truein
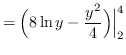
truein
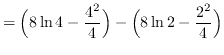
truein
![]()
truein
![]()
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 9: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() and
and ![]() .
.
trueintruein
SOLUTION 9: Compute the area of the enclosed
region bounded by the graphs of the equations ![]() and
and ![]() . Begin by finding the points of intersection of the
two graphs. From
. Begin by finding the points of intersection of the
two graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
![]() or
or ![]()
![]()
truein
![]() or
or ![]()
truein
Using vertical cross-sections we get that
truein
AREA
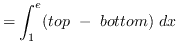
truein
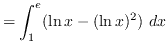
truein
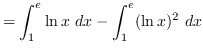
truein
Let
![]() and
and
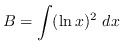 .
.
truein
(Recall from PROBLEM 6 that
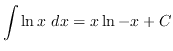 )
)
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
Use integration by parts. Let
![]() and
and ![]() such that
such that
![]() and
and ![]() .
.
truein
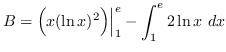
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 10: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() ,
, ![]() and
and
![]() .
.
trueintruein
SOLUTION 10: Compute the area of the
enclosed region bounded by the graphs of the equations ![]() ,
, ![]() , and
, and ![]() . Begin by finding the points
of intersection of the two graphs. From
. Begin by finding the points
of intersection of the two graphs. From
![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
Using vertical cross-sections we get that
truein
AREA
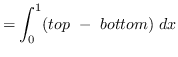
truein
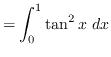
truein
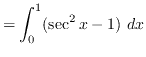
truein
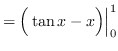
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 11: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() and
and ![]() .
.
trueintruein
SOLUTION 11: Compute the area of the
enclosed region bounded by the graphs of the equations ![]() ,
, ![]() , and
, and ![]() . Begin by finding the points of
intersection of the two graphs.
. Begin by finding the points of
intersection of the two graphs.
truein
From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
Using vertical cross-sections we get that
truein
AREA
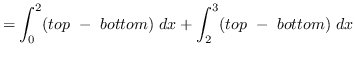
truein
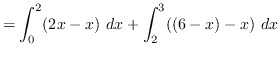
truein
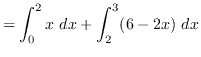
truein
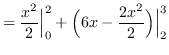
truein
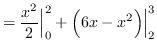
truein
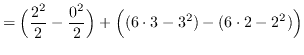
truein
![]()
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 12: Compute the area of the enclosed region
bounded by the graphs of the equations
![]() ,
, ![]() , and
, and ![]() .
.
trueintruein
SOLUTION 12: Compute the area of the
enclosed region bounded by the graphs of the equations
![]() ,
, ![]() , and
, and ![]() . Begin by finding the
points of intersection of the two graphs. From
. Begin by finding the
points of intersection of the two graphs. From
![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
Using vertical cross-sections we get that
truein
AREA
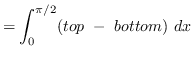
truein
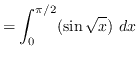
truein
Use integration by parts. Let
![]() and
and
![]() such that
such that
![]() and
and ![]() .
.
truein
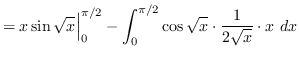
truein
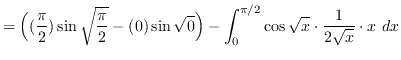
truein
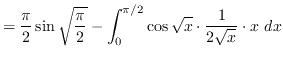
truein
Use substitution. Let
truein
![]()
truein
so that
truein
![]()
truein
![]()
truein
![]()
truein
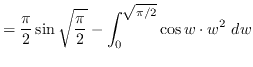
truein
Use integration by parts. Let ![]() and
and
![]() such that
such that ![]() and
and ![]() .
.
truein
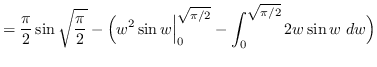
truein
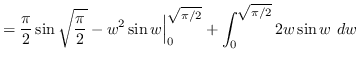
truein
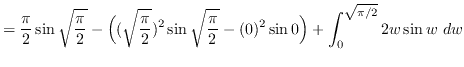
truein
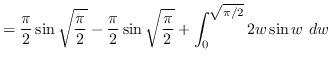
truein
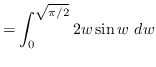
truein
Use integration by parts. Let ![]() and
and
![]() such that
such that ![]() and
and ![]()
truein
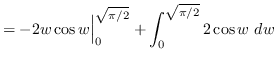
truein
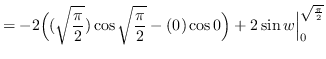
truein
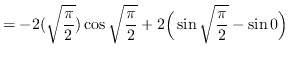
truein
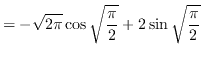
trueintrueintruein
PROBLEM 13: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() and
and ![]() .
.
trueintruein
SOLUTION 13: Compute the area of the
enclosed region bounded by the graphs of the equations ![]() and
and ![]() . Begin by finding the points of intersection of the
two graphs. From
. Begin by finding the points of intersection of the
two graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]() or
or ![]()
truein
Using horizontal cross-sections we get that
truein
AREA
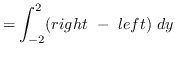
truein
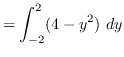
truein
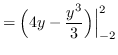
truein
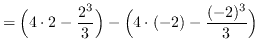
truein
![]()
truein
![]()
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 14: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() and
and ![]() .
.
trueintruein
SOLUTION 14: Compute the area of the
enclosed region bounded by the graphs of the equations ![]() and
and ![]() . Begin by finding the points of intersection of
the two graphs. From
. Begin by finding the points of intersection of
the two graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
![]() or
or ![]()
truein
Using horizontal cross-sections we get that
truein
AREA
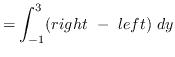
truein
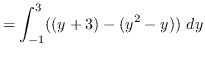
truein
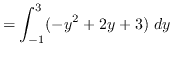
truein
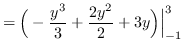
truein
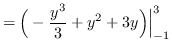
truein
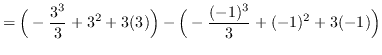
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()
trueintrueintruein
PROBLEM 15: Compute the area of the enclosed region
bounded by the graphs of the equations ![]() and
and ![]() .
.
trueintruein
SOLUTION 15: Compute the area of the
enclosed region bounded by the graphs of the equations ![]() and
and ![]() . Begin by finding the points of intersection
of the two graphs. From
. Begin by finding the points of intersection
of the two graphs. From ![]() and
and ![]() we get that
we get that
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]() ,
, ![]() , or
, or ![]()
truein
Using horizontal cross-sections we get that
truein
AREA
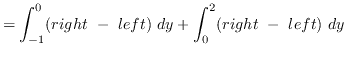
truein
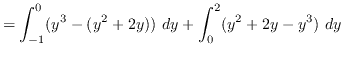
truein
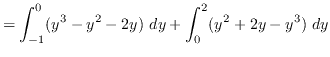
truein
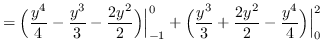
truein
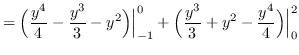
truein
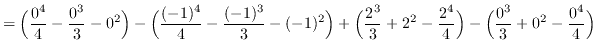
truein
![]()
truein
![]()
truein
![]()
truein
![]()
truein
![]()