Research Summary- Jesús Antonio De Loera.

I started my career working in convex & discrete geometry, and computational geometry. My work in the combinatorics and geometry of convex polytopes is well-known. In my dissertation, I solved an open question of well-known mathematicians Gelfand, Kapranov and Zelevinsky by finding an example of a non-regular triangulation of the cartesian product of two simplices and later worked very deeply on the problem of finding optimal triangulations of polyhedra (e.g., I proved that the minimum triangulation of the dodecahedron has 23 tetrahedra). My first book (joint with Rambau and Santos) Triangulations: Structures for Algorithms and Applications published by Springer in 2010, is a thorough reference about triangulations of polyhedra. I have also published many noteworthy contributions to the problems of computing volumes and integrals of polyhedra, and about counting lattice points. The list of applications of these computational problems is very large, algebraic geometry and representation theory (toric varieties, Clebsch-Gordan coefficients) to combinatorics, computer algebra, and statistics (E.g., in joint work with Liu and Yoshida we found the first ever closed-form combinatorial formula for the volumes and of the Birkhoff polytope $B_n$, i.e., the convex hull of all $n \times n$ permutation matrices). I have also contributed to understanding Ehrhart polynomials and the well-known software LattE was started under my direction and initiative, introducing dozens of undergraduates to research.

Although I continue to be interested in my earlier topics, most of my work in the past seven years has been in the applied area of integer and combinatorial optimization. This is the part of applied mathematics related to optimizing functions over discrete sets. A famous example of such problem is the traveling salesman problem: Given $n$ cities that must be visited only once, and the costs $c_{ij}$ of flying from city $i$ to city $j$, the goal is to find the best order to visit all the given cities in order to minimize the total cost of the trip.

I have been one of the leaders of a new approach to the theory of optimization. In this new point of view, tools from algebra, topology and geometry, that were considered too pure and unrelated to applications, are used to prove unexpected computational or structural results. My new second book (joint with Hemmecke and Köppe) Algebraic and Geometric Ideas in the theory of Discrete Optimization is the first compilation of results from this novel approach collecting the work of several mathematicians. My own work has provided fundamental new developments taking place in the area of discrete optimization which I summarize here:

1. Traditionally the theory is concentrated on how to solve problems with only linear equations or constraints. In pioneering work published in 2006, joint with Hemmecke, Köppe and Weismantel) we proved the first theoretical results for the more difficult model with non-linear objective functions. To put them in context, let me recall that one of the most famous results for the theory of integer programming, obtained by H.W. Lenstra Jr. in 1983, states that when the number of variables is fixed and both the objective function $f$ and constraints $g_i$ are linear polynomials, then there is an algorithm to solve it in polynomial time on the input size. Similarly, another famous breakthrough, in 2002, L. Khachiyan and L.Porkolab proved that the same holds when the number of variables is fixed and the objective $f$ is a convex polynomial. It is thus a natural question to ask: if we continue to fix the number of variables and the $g_i$ are linear, but the objective function $f$ is an arbitrary non-linear polynomial, what is the computational complexity?

   We extended the Lenstra's and Khachiyan's results, we answered the question in a paper appeared in Mathematics of Operations Research: We proved that while the problem is NP-hard, even for fixed dimension 2, there is a new approximation algorithm to maximize an arbitrary integral polynomial over the lattice points of a convex rational polytope with a fixed dimension. The algorithm produces a sequence of upper and lower bounds for the global optimal value. Surprisingly this is an excellent approximation scheme. The new method codifies the (exponentially many) lattice point solutions, as a short (polynomial-size) multivariate rational generating function (sum of quotients of polynomials). This result was nominated to various awards the year of 2006 when it was published, including the Fulkerson Prize. Later Hemmecke, Köppe and I showed that igives a similar result for multiobjective optimization.

2. An integer linear program (ILP) is the problem of finding, for given matrix $A$ and vectors $b,c$, the minimum $min \{cx : Ax=b, \ x\geq 0 \ \hbox{integer} \}$. The problem is well-known to be NP-hard; thus one does not expect that a general efficient algorithm can be found. For an ILP $P_b=min \{cx : Ax=b, \ x\geq 0 \ \hbox{integer}\}$ a test set is a finite set of integral vectors such that every feasible non-optimal solution can be improved by adding a vector from the test set. The lattice $L(A)=\{x \in {\mathbb{Z}}^n : Ax=0\}$ has a natural partial order. For $u,v\in {\mathbb{Z}}^n$ we say that $u$ is conformal to $v$, denoted $u\sqsubset v$, if $\vert u_i\vert\leq \vert v_i\vert$ and $u_iv_i\geq 0$ for $i=1,\ldots,n$, that is, $u$ and $v$ lie in the same orthant of ${\mathbb{R}}^n$ and each component of $u$ is bounded by the corresponding component of $v$ in absolute value. The Graver basis of an integer matrix $A$ is the set of conformal-minimal nonzero integer dependencies on $A$. For example, if $A=[1\ 2\ 1]$ then its Graver basis is $\pm \{ [2,-1,0],[0,-1,2],[1,0,-1],[1,-1,1]\}$.

   Graver bases are in fact connected to commutative algebra and algebraic geometry, they are a universal Gröbner bases for the toric ideal associated to the matrix $A$. During the past fifteen years, algebraic geometry and commutative algebra tools have been shown exciting potential to study problems in integer optimization. But, in the past, algebraic methods had always been considered ``guilty'' of bad computational complexity, namely, the notorious bad complexity for computing general Gröbner bases when the number of variables grow. Our exciting new research demonstrated that, by carefully using the structure of matrix $A$, Graver bases can compete (and win!!!) against mainstream tools in optimization. The paper appeared in the journal Discrete Optimization:

   Fix any pair of integer matrices $A$ and $B$ with the same number of columns, of dimensions $r\times q$ and $s\times q$, respectively. The n-fold matrix of the ordered pair $A,B$ is the following $(s+nr)\times nq$ matrix,

   $$[A,B]^{(n)} \quad:=\quad ({\bf 1}_n\otimes B)\oplus (I_n\otim... ...dots \\ 0 & 0 & 0 & \cdots & A \\ \end{array}\right)\quad .$$

   The number of variables grow, but we can prove

   Theorem Fix any integer matrices $A,B$ of sizes $r\times q$ and $s\times q$, respectively. Then there is a polynomial time algorithm that, given any $n$ and any integer vectors $b$ and $c$, solves the corresponding n-fold integer programming problem.

   $$\min\{cx:\ [A,B]^{(n)}x=b,\ x\in{\mathbb{N}}^{nq}\}\quad.$$

   The key ingredient to make it work comes from commutative algebra. What happens is that for every pair of integer matrices $A\in {\mathbb{Z}}^{r\times q}$ and $B\in {\mathbb{Z}}^{s\times q}$, there exists a constant $g(A,B)$ such that for all $n$, the Graver basis of $[A,B]^{(n)}$ consists of vectors with at most $g(A,B)$ the number nonzero components. This means that it suffices to compute the Graver bases of a small $n$-fold matrix to be able to obtain others. More recently we were also able to extend the above theorem to the optimization of maximization convex functions instead of just optimizing linear functions.

3. An important family of integer linear programs are the multi-index transportation problems. These polytopes consist of all real-valued tables, arrays whose entries satisfies given sums from the entries (e.g., row sums, column sums equal to some values). Transportation polytopes, their integer points (called contingency tables by statisticians), and their projections, have been used and appear extensively in the operations research literature due to their importance on scheduling and planning. Their name was coined by Nobel-prize winner economist T. Koopmans who was interested on the efficient transportation of good by ships.

   Back in 1986 several open problems were proposed by Vlach and co-authors. 20 year later, in our paper published in the SIAM Journal of Optimization, S. Onn and I solved most of them as easy corollaries of the following theorem

   Theorem: (De Loera-Onn) Any integer programming problem $\hbox{maximize}\{cy : y\mathbb{R}_{\geq 0}^n, \ Ay=b\}$ is in fact polynomial-time representable as a $3$-way transportation problem with $2$-marginals $w,v,u$ depending polynomially on the binary size of the input $A,b,c$:

   $$\hbox{maximize}\{\,cx:\ \mathbb{R}_{\geq 0}^{r\times c\times 3}\ ... ...j,k}=w_{j ,k}\,,\ \sum_j x_{i,j,k}=v_{i,k}\,,\ \sum_k x_{i,j,k}=u_{i,j}\,\}\ .$$

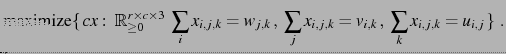
   By saying that an integer program is representable as another we mean that the solution spaces are identical and one can transfer one into the other efficiently. Thus, one can interpret our theorem as a ``normal form'' or ``canonical reformulation'' algorithm. So, any integer or linear programming problem can be put in the special form of a multiway transportation problems for arrays of 3 indices with line sums prescribed.

4. In 2010 I received the INFORMS computer society award (ICS prize). The ICS Prize is an annual award for best English language paper or group of related papers dealing with the Operations Research/Computer Science interface. INFORMS (The Institute for Operations Research and the Management Sciences) is the largest international organization dedicated to operations research and the science of management, i.e., the application of advanced mathematical methods to help make better decisions in society. Here is what the prize citation says about these two winning papers:

   ``These two papers introduce a pioneering new approach for proving the optimality of solutions to combinatorial optimization problems. The approach begins by encoding the instance and an objective bound as a system of polynomial equations over a finite field. Then, using Hilbert's Nullstellensatz, the authors demonstrate the effectiveness of a computational method to certify the infeasibility of the polynomial system. The encoding is derived and analyzed for a number of problem classes, such as the k-coloring, stable set, longest cycle, largest planar subgraph, and minimum edge coloring problems. While the degree of the certifying polynomial could be exponentially large, the authors demonstrate that in many cases of interest the degree is low enough to allow for explicit, fast computations. The authors also develop a variety of computational enhancements, including computing over finite fields, exploiting symmetry, adding redundant equations, and applying alternative Nullstellensätze that allow them to solve 3-coloring problems significantly faster than existing methods.

   In this impressive work, the authors take up a mathematical machinery that seemed very unlikely to be useful in practice and turn it into a useful computational algorithm. This work is likely to stimulate additional research into computational polynomial methods, perhaps placing them on the same footing as polyhedral techniques for solving combinatorial optimization problems.''

5. Most recently, I have been an active contributor in the study of the complexity of linear optimization algorithms, most notably, the simplex method and interior point methods. The central path is the key object in interior point methods algorithms and software. In joint work with Vinzant and Sturmfels, we solved that 20-year-old problem, by giving explicit exact algebraic formulas for the central path, determined the degree, and genus of the curve. These invariants, along with the degree of the Gauss image of the curve, are expressed in terms of a matroid of the input data. As an application we give an instance-specific bound of the total curvature of the central path, a quantity relevant for the performance of interior point methods. The key mathematical ``liaison'' we managed to established is that the differential geometry of a central curve is intimately connected to that of the underlying matroid of the constraints.

   Another significant contribution regards the geometry of the simplex method. It is of course a long-standing open question to bound the diameter of the graphs of convex polyhedra. It is well-known in linear optimization that bounding the diameter is important for the performance of the simplex, which searches the graph of the polyhedron. Fields medalist Steven Smale has listed the problem of finding a strongly polynomial algorithm for linear programming, possibly via a polynomial pivot rule for the simplex method, as one of the key mathematical problems in the 21st century. Billera and Provan had proposed in 1979 a conjecture that if true would have proved a linear bound to the diameter of all polyhedra, namely twice the number of facet defining inequalities. The idea relies on a clever decomposition of simplicial complexes by a sequence of removals of lower dimensional faces. In a very recent paper published in Mathematics of Operation Research in 2012 (joint work with former postdoc Steve Klee), we solve their open question about their method to bound the diameter of convex polyhedra on the negative. We disproved the conjecture showing that the conjecture fails in a 4-dimensional example coming from transportation optimization problems. The construction is very elegant and uses topological tools (e.g., simplicial complexes deletion and contraction of edges).