Why You Cannot Divide by Zero - January 2025

Kyle R. Chickering

[ Homepage ]

In my undergraduate courses, especially the calculus series, I see lots of students who wish to divide by zero and then proceed to do so, often guessing at what the resulting answer should be! In this short blog post I hope to convince you that dividing by zero does not make mathematical sense, and that if you encounter division by zero something has gone wrong!

First, what is division? $\frac{a}{b}=c$ means that if you multiply $c$ by $b$ you get $a$, that is $a=bc$. Supposing that $b=0$ and $c \ne 0$, this of course means that $a=0$. One might naïvely then suppose that $\frac{0}{0}=0$, but this is not actually true. Why not? Well, I said that division is $\frac{a}{b}=c$, but I left out a crucial piece of information: this definition is only allowed if $b\ne 0$!

Why can’t we simply define $\frac{0}{0}=0$? Well, consider the function

We ask the following question: what is the value of $f(0)$? In calculus you learn some clever ways of computing this, but let us simply plug in $0$. What do we get?

Easy! So $f(0)=0$, right? No! If you look at the graph of $f(x)$ you will see that $f(0)=1$!

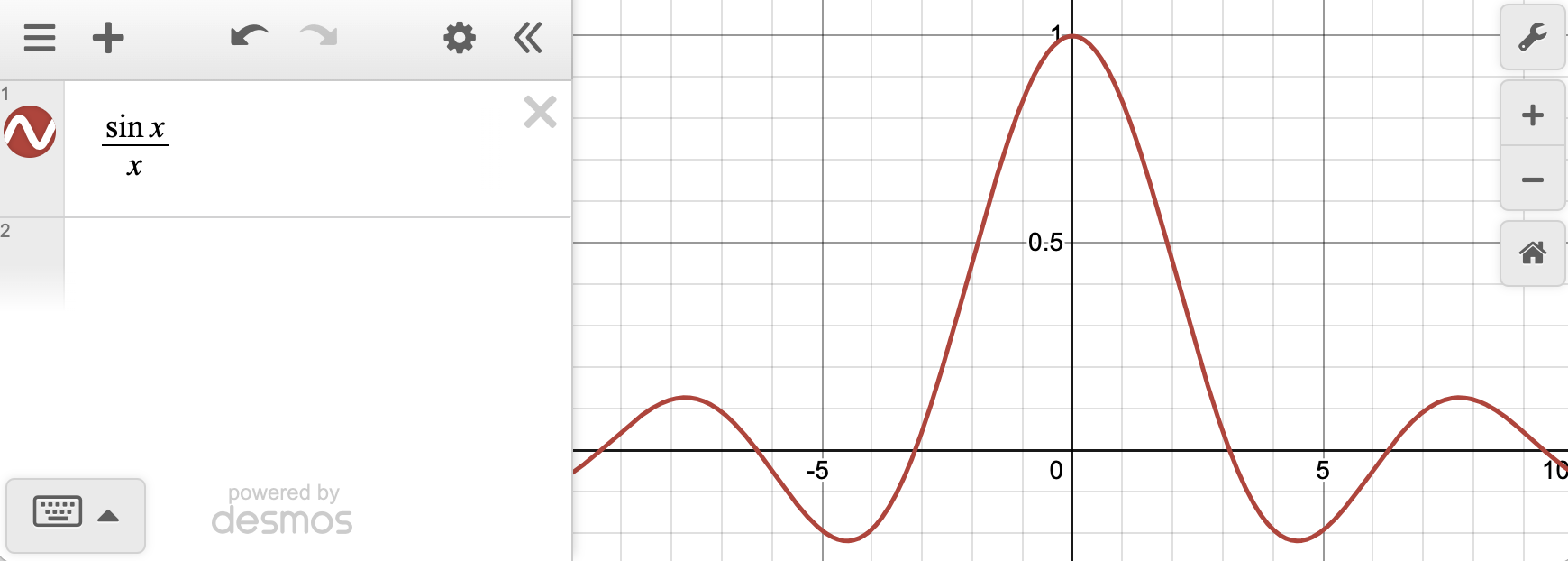
Let’s go back to our multiplication example. When $xf(x)=\sin(x)$ we are asking what is the value of $f(x)$ to make $0\times f(0)=0$? The answer: anything! Thus, the equation $f(0)=\frac{0}{0}$ doesn’t tell us anything. So that is why you cannot divide by zero, it’s an indefinite equation, it means you’re missing some piece of information!

As you continue with your calculus journey you will learn that the explanation I have given here glosses over a lot of nuance, and for that I apologize. I hope that this simple example convinces you that division by zero is not allowed. If you find yourself dividing by zero you should look over your work and check for algebra errors!