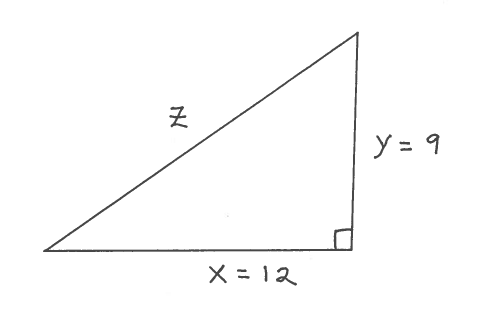Related Rates Problems

Processing math: 100%

Solving Related Rates Problems

The following problems involve the concept of Related Rates. In short, Related Rates problems combine word problems together with Implicit Differentiation, an application of the Chain Rule. Recall that if $y=f(x)$ , then $D \{y \} = \displaystyle{ dy \over dx } = f'(x)=y'$ . For example, implicitly differentiating the equation $y^3+y^2= y+1$ would be $D\{y^3+y^2\} = D\{ y+1 \} \ \ \ \ \longrightarrow$ $3y^2 \cdot y'+ 2y \cdot y' = y' + 0$ If $x=f(t)$ and $y=g(t)$ , then $D\{x\} = \displaystyle{ dx \over dt } = f'(t)$ and $D\{y\} = \displaystyle{ dy \over dt } = g'(t)$ . For example, implicitly differentiating the equation $x^3+y^2= x+y+3$ would be $D\{x^3+y^2\} = D\{ x+y+3 \} \ \ \ \ \longrightarrow$ $3x^2 \cdot \displaystyle{ dx \over dt } + 2y \cdot \displaystyle{ dy \over dt } = \displaystyle{ dx \over dt } + \displaystyle{ dy \over dt } + 0$

In all of the following Related Rates Problems, it will be assumed that each variable function $y$ is a function of time $t$ . For that reason, I will always use Leibniz notation and not the ambiguous prime notation for derivatives, i.e., i will use $\displaystyle{ dy \over dt } \ \ \ \ instead \ of \ \ \ \ y'$ Here is my strategy for approaching and solving Related Rates Problems:

1.) Read the problem slowly and carefully.
2.) Draw an appropriate sketch.
3.) Introduce and define appropriate variables. Use variables if quantities are changing. Use constants if quantities are not changing.
4.) Read the problem again.
5.) Clearly label the sketch using your variables.
6.) State what information is given in the problem.
7.) State what information is to be determined or found.
8.) Use a given equation or create an appropriate equation relating the given variables.
9.) Differentiate this equation with respect to the time variable $t$ .
10.) Plug in the given rates and numbers to the differentiated equation.
11.) Solve for the unknown rate.
12.) Put proper units on your final answer.

EXAMPLE 1: Consider a right triangle which is changing shape in the following way. The horizontal leg is increasing at the rate of

$5 \ in./min.$ and the vertical leg is decreasing at the rate of

$6 \ in./min$ . At what rate is the hypotenuse changing when the horizontal leg is

$12 \ in.$ and the vertical leg is

$9 \ in.$ ?

Draw a right triangle with legs labeled

$x$ and

$y$ and hypotenuse labeled

$z$ , and assume each edge is a function of time

$t$ .

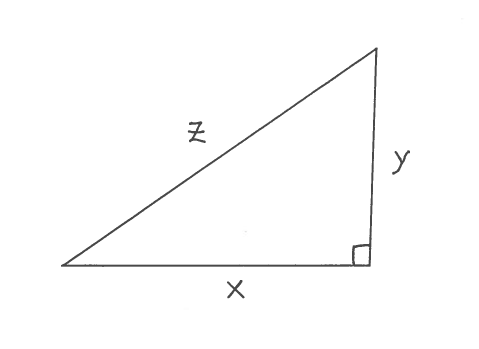
tex2html_wrap_inline125

GIVEN:

$\ \ \ \displaystyle{ dx \over dt } = 5 \ in./min. \$ and

$\ \displaystyle{ dy \over dt }= -6 \ in./min.$

FIND:

$\ \ \ \displaystyle{ dz \over dt }$ when

$x=12 \ in.$ and

$y=9 \ in$ .

Use the Pythagorean Theorem to get the equation

$x^2 + y^2 = z^2$

Now differentiate this equation with repect to time

$t$ getting

$D \{ x^2 + y^2\} = D \{z^2\} \ \ \ \longrightarrow$

$2x \displaystyle{ dx \over dt } + 2y \displaystyle{ dy \over dt } = 2z \displaystyle{ dz \over dt } \ \ \ \longrightarrow \ \$ (Multiply both sides of the equation by

$1/2$ .)

$x \displaystyle{ dx \over dt } + y \displaystyle{ dy \over dt } = z \displaystyle{ dz \over dt } \ \ \ \ \ \ \ \ \ \ \ \ \ \ (DE)$ Now let

$x=12$ and

$y=9$ and solve for

$z$ using the Pythagorean Theorem.

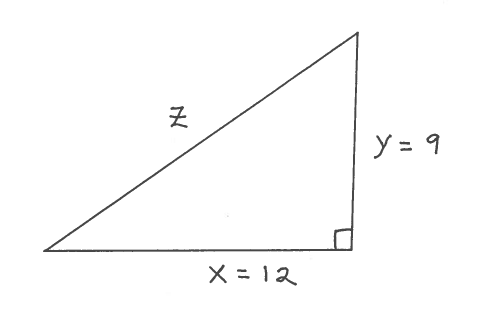
tex2html_wrap_inline125

$12^2+9^2= z^2 \ \ \ \longrightarrow \ \ \ z^2=225 \ \ \ \longrightarrow \ \ \ z=15$ Plug in all given rates and values to the equation

$(DE)$ getting

$(12)(5) + (9)(-6) = (15) \displaystyle{ dz \over dt } \ \ \ \longrightarrow$

$6 = 15 \displaystyle{ dz \over dt } \ \ \ \longrightarrow$

$\displaystyle{ dz \over dt } = {6 \over 15} = { 2 \over 5} \ in/min.$

In the list of Related Rates Problems which follows, most problems are average and a few are somewhat challenging.

PROBLEM 1 : The edge of a square is increasing at the rate of $\ 3 \ cm/sec$ . At what rate is the square's

$\ \ \ \$ a.) perimeter changing
$\ \ \ \$ b.) area changing

when the edge of the square is $10 \ cm.$ ?
Click HERE to see a detailed solution to problem 1.
PROBLEM 2 : The length of a rectangle is increasing at the rate of $\ 4 \ ft/hr.$ and the width of the rectangle is decreasing at the rate of $\ 3 \ ft/hr.$ At what rate is the rectangle's

$\ \ \ \$ a.) perimeter changing
$\ \ \ \$ b.) area changing

when the length is $\ 8 \ ft.$ and the width is $\ 5 \ ft.$ ?
Click HERE to see a detailed solution to problem 2.
PROBLEM 3 : Leg one of a right triangle is decreasing at the rate of $\ 5 \ in/sec.$ and leg two of the right triangle is increasing at the rate of $\ 7 \ in/sec.$ At what rate is the triangle's

$\ \ \ \$ a.) hypotenuse changing
$\ \ \ \$ b.) perimeter changing
$\ \ \ \$ c.) area changing

when leg one is $\ 8 \ in.$ and leg two is $\ 6 \ in.$ ?
Click HERE to see a detailed solution to problem 3.
PROBLEM 4 : The radius of a circular oil slick on the surface of a pond is increasing at the rate of $\ 10 \ meters/min.$ At what rate is the circle's

$\ \ \ \$ a.) circumference changing
$\ \ \ \$ b.) area changing

when the radius of the oil slick is $\ 20 \ m.$ ?
Click HERE to see a detailed solution to problem 4.
PROBLEM 5 : A big block of ice is in the shape of a perfect cube. As it melts, each edge of the cube is decreasing at the rate of $\ 2 \ cm/min.$ At what rate is the ice cube's

$\ \ \ \$ a.) surface area changing
$\ \ \ \$ b.) volume changing

when the edge of the ice cube is $\ 80 \ cm.$ ?
Click HERE to see a detailed solution to problem 5.
PROBLEM 6 : A ladder 13 feet long is leaning against a high wall. If the base of the ladder is pushed toward the wall at the rate of $\ 2 \ ft/sec.$ , at what rate is the top of the ladder moving up the wall when the base of the ladder is

$\ \ \ \$ a.) 5 feet
$\ \ \ \$ b.) 1 foot

from the wall ?
Click HERE to see a detailed solution to problem 6.
PROBLEM 7 : The radius of a large sphere is increasing at the rate of $\ 3 \ ft/hr.$ At what rate is the sphere's

$\ \ \ \$ a.) surface area changing
$\ \ \ \$ b.) volume changing

when the radius of the sphere is $\ 10 \ ft.$ ?
Click HERE to see a detailed solution to problem 7.
PROBLEM 8 : Consider a closed right circular cylinder of base radius $r \ cm.$ and height $h \ cm.$ If the radius of the cylinder is increasing at the rate of $\ 5 \ cm/hr.$ and the height of the cylinder is decreasing at the rate of $\ 4 \ cm/hr.$ , at what rate is the sphere's

$\ \ \ \$ a.) surface area changing
$\ \ \ \$ b.) volume changing

when the radius of the cylinder is $\ 20 \ cm.$ and the height of the cylinder is $12 \ cm.$ ?
Click HERE to see a detailed solution to problem 8.
PROBLEM 9 : Consider the given isosceles triangle of base 10 inches and side lengths $x$ inches. If $x$ is increasing at the rate of $\ 4 \ in/min.$ , at what rate is the triangle's

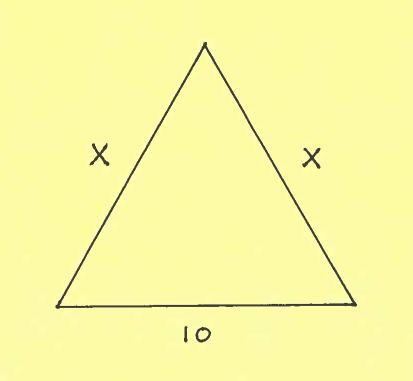
$\ \ \ \$ a.) perimeter changing
$\ \ \ \$ b.) height changing
$\ \ \ \$ c.) area changing

when $x=13 \ in.$ ?
Click HERE to see a detailed solution to problem 9.
PROBLEM 10 : Consider the given closed rectangular box with dimensions $x$ feet by $y$ feet by $z$ feet. Assume that $x$ is increasing at the rate of $\ 4 \ ft/hr.$ , $y$ is decreasing at the rate of $\ 6 \ ft/hr.$ , and $z$ is increasing at the rate of $\ 3 \ ft/hr.$ At what rate is the box's

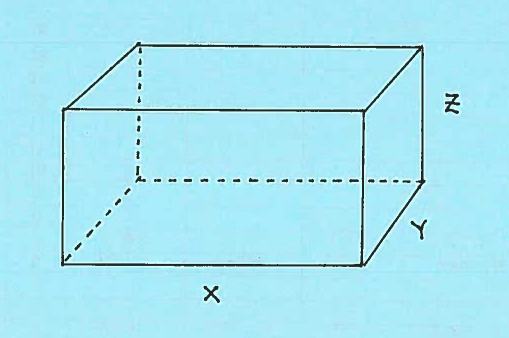
$\ \ \ \$ a.) surface area changing
$\ \ \ \$ b.) volume changing
$\ \ \ \$ c.) main diagonal changing

when $x=5 \ ft.$ , $y=4 \ ft.$ , and $z=6 \ ft.$ ?
Click HERE to see a detailed solution to problem 10.
PROBLEM 11 : The volume of a large spherical balloon is increasing at the rate of $\ 64 \pi \ meters^3/hr. \approx 201.06 \ meters^3/hr.$ At what rate is the balloon's surface area changing when the radius of the balloon is $\ 2 \ m.$ ?
Click HERE to see a detailed solution to problem 11.
PROBLEM 12 : The surface area of a cube is increasing at the rate of $\ 600 \ in^2/hr.$ At what rate is the cube's volume changing when the edge of the cube is $\ 10 \ in.$ ?
Click HERE to see a detailed solution to problem 12.
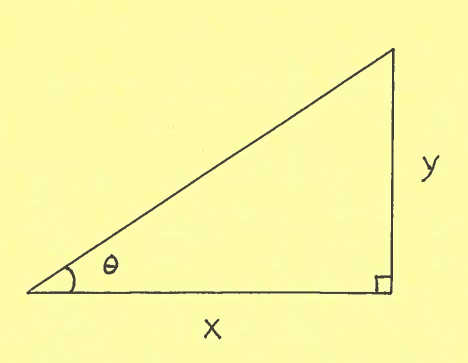
PROBLEM 13 : Consider the given right triangle with legs of length $x \ cm.$ and $y \ cm.$ and angle $\theta$ radians. If $x$ is decreasing at the rate of $\ 3 \ cm/min.$ and $y$ is increasing at the rate of $\ 4 \ cm/min.$ , at what rate is angle $\theta$ changing when $x=5 \ cm.$ and $y=2 \ cm.$ ?

Click HERE to see a detailed solution to problem 13.
PROBLEM 14 : You are sitting $x \ ft.$ from a wall and watching a movie screen which is 10 feet high and is 6 feet above the floor. Your viewing angle is $\theta$ radians. (See the side view diagram below.)

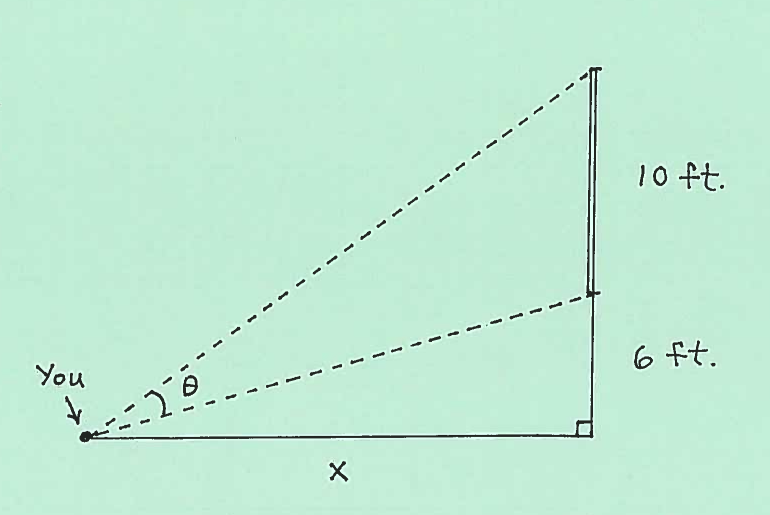
a.) Write your viewing angle $\theta$ as a function of $x$ .
b.) If x is increasing at the rate of $\ 10 \ ft/min.$ , at what rate is $\theta$ changing when

$\ \ \ \ \ \ i.) \ x=8 \ ft.$ ?
$\ \ \ \ \ \ i.) \ x=20 \ ft.$ ?
Click HERE to see a detailed solution to problem 14.
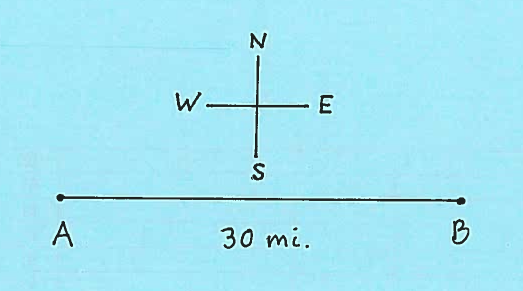
PROBLEM 15 : Car B starts 30 miles directly east of car A and begins moving west at 90 mph. At the same moment car A begins moving north at 60 mph. At what rate is the distance between the cars changing after

$\ \ \ \ \ \$ a.) $t = 1/5 \ hr.$ ?
$\ \ \ \ \ \$ b.) $t = 1/3 \ hr.$ ?

Click HERE to see a detailed solution to problem 15.
PROBLEM 16 : An open right circular conical tank (vertex down) has height 10 meters and base radius 8 meters. Water begins flowing into the tank at the rate of $\ \pi \ meters^3/min.$ At what rate is the depth $h$ of the water in the tank changing when

$\ \ \ \ \ \$ a.) $h = 1 \ m.$ ?
$\ \ \ \ \ \$ b.) $h = 9 \ m.$ ?

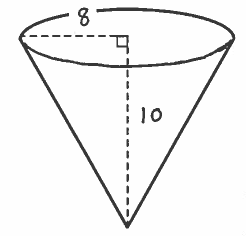
Click HERE to see a detailed solution to problem 16.
PROBLEM 17 : An open hemispherical tank has radius 13 feet. Oil begins flowing into the tank in such a way that the depth $h$ of the oil in the tank changes at the rate of $3 \ ft/hr.$ At what rate is the top circular surface area of the oil changing when the depth of oil is

$\ \ \ \ \ \$ a.) $h = 1 \ ft.$ ?
$\ \ \ \ \ \$ b.) $h = 8 \ ft.$ ?

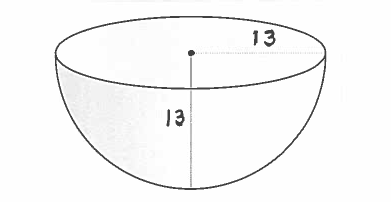
Click HERE to see a detailed solution to problem 17.
PROBLEM 18 : Car 1 starts on the graph of $y=e^x$ at the point $(0,1)$ , and car 2 starts on the graph of $y=3x-2$ at the point $(0,-2)$ and distance is measured in miles. If both cars start moving to the right at the same time in such a way that $\displaystyle{ dx \over dt } = 1 \ mile/min.$ , at what rate is the distance between the cars changing when

$\ \ \ \ \ \$ a.) $t = 1 \ min.$ ?
$\ \ \ \ \ \$ b.) $t = 3 \ min.$ ?

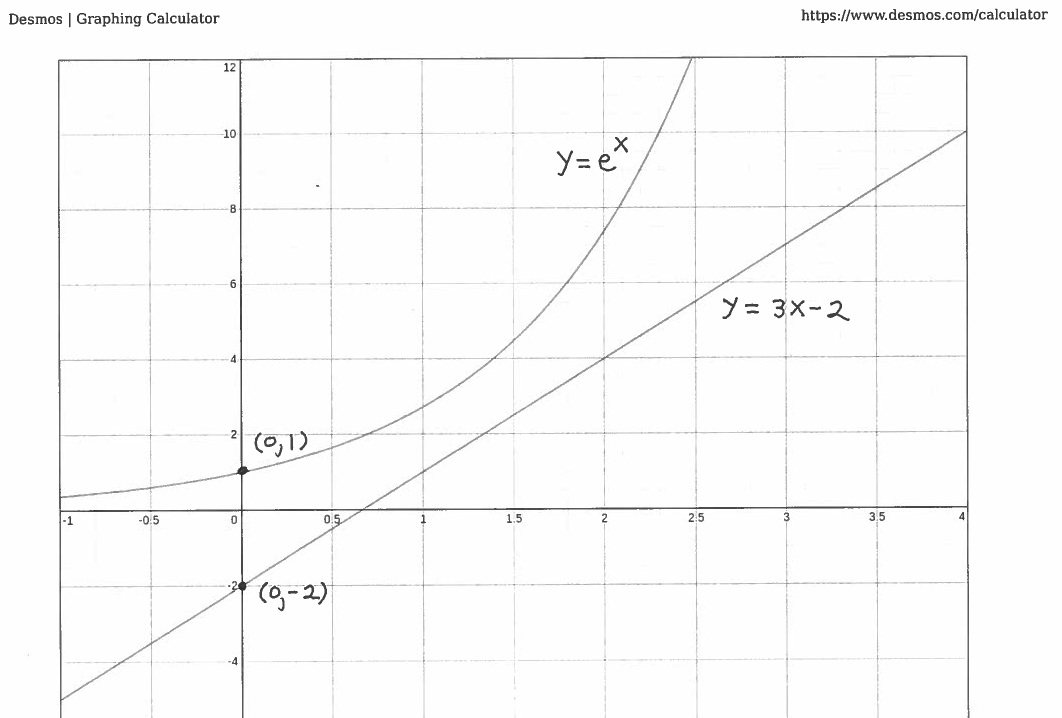
Click HERE to see a detailed solution to problem 18.
PROBLEM 19 : You are standing 12 feet from the base of a 200-ft. cliff. As a boulder rolls off the cliff, you begin running away at $10 \ ft/sec.$ At what rate is the distance between you and the boulder changing after

$\ \ \ \ \ \$ a.) $t = 1 \ sec.$ ?
$\ \ \ \ \ \$ b.) $t = 3 \ sec.$ ?

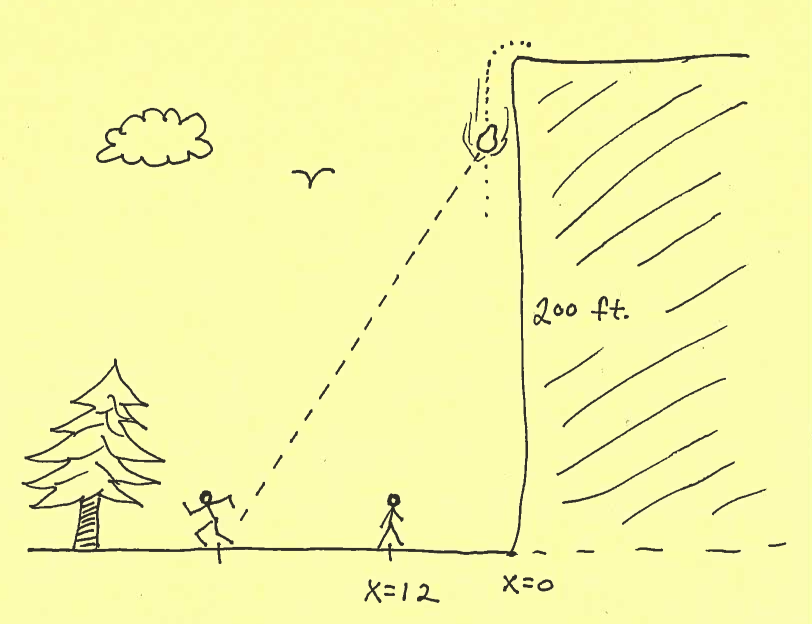
Click HERE to see a detailed solution to problem 19.

Click HERE to return to the original list of various types of calculus problems.

Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :

kouba@math.ucdavis.edu

A heartfelt "Thank you" goes to The MathJax Consortium for making the construction of this webpage fun and easy.

Duane Kouba ... October 24, 2019