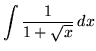 . Use the power substitution
. Use the power substitution
![]()
so that
![]()
and
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
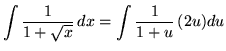
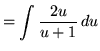
(Use polynomial division.)
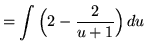

![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 2 : Integrate
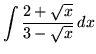 . Use the power substitution
. Use the power substitution
![]()
so that
![]()
and
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
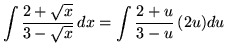
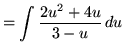
(Use polynomial division.)
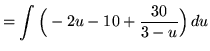

![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 3 : Integrate
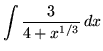 . Use the power substitution
. Use the power substitution
![]()
so that
![]()
and
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
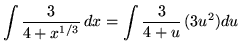
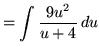
(Use polynomial division.)



![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 4 : Integrate
 . Use the power substitution
. Use the power substitution
![]()
so that
![]() ,
,
![]() ,
,
and
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
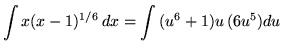
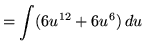
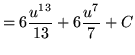
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 5 : Integrate
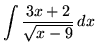 . Use the power substitution
. Use the power substitution
![]()
so that
![]() ,
,
![]() ,
,
and
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
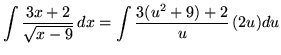
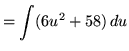
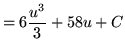
![]()
![]()
![]() .
.
Click HERE to return to the list of problems.
SOLUTION 6 : Integrate
 . Use the power substitution
. Use the power substitution
![]()
so that
![]() ,
,
![]() ,
,
and
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
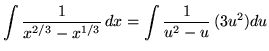
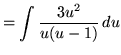

(Use polynomial division.)
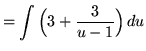
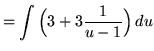
![]()
![]() .
.
Click HERE to return to the list of problems.