![]()
and
![]() .
.
The method of power substitution assumes that you are familiar with the method of ordinary u-substitution and the use of differential notation. Recall that if
![]() ,
,
then
![]() .
.
For example, if
![]() ,
,
then
![]() .
.
When using the method of power substitution, we will usually assume that
![]() ,
,
so that
![]() .
.
For example, if
![]() ,
,
then
![]() .
.
The goal of a power substitution will be to replace ![]() th roots of functions, which may not be easily integrated, with integer powers of functions, which are more easily integrated. For example, if we start with the expression
th roots of functions, which may not be easily integrated, with integer powers of functions, which are more easily integrated. For example, if we start with the expression
![]()
and let
![]() ,
,
then
![]()
and
![]() .
.
Thus,
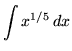
could be rewritten as
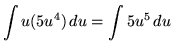 .
.
In general, to eliminate
![]() ,
,
let
![]() .
.
Then
![]()
and
![]() .
.
Recall the following well-known, basic indefinite integral formulas :
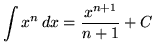 , where
, where 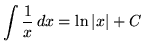
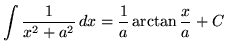
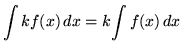 , where
, where 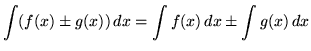
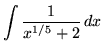 .
.
A COMMON WRONG ANSWER FOR THIS PROBLEM IS
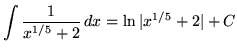 .
.
Convince yourself that the answer is wrong by differentiating the right-hand side and showing it is NOT equal to the function on the left-hand side of the above equation. To properly integrate this problem, use the power substitution
![]()
so that
![]()
and
![]() .
.
Now substitute into the original problem, replacing all forms of ![]() , getting
, getting
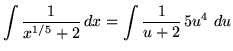
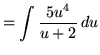
(Use polynomial division.)
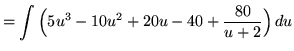
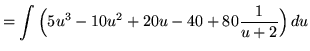
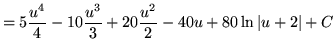
![]()
![]() .
.
Most of the following problems are average. A few are challenging. Make careful and precise use of the differential notation ![]() and
and ![]() and be careful when arithmetically and algebraically simplifying expressions. You will likely need to use the following rules for exponents.
and be careful when arithmetically and algebraically simplifying expressions. You will likely need to use the following rules for exponents.
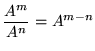
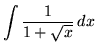 .
.
Click HERE to see a detailed solution to problem 1.
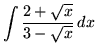 .
.
Click HERE to see a detailed solution to problem 2.
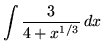 .
.
Click HERE to see a detailed solution to problem 3.
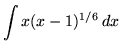 .
.
Click HERE to see a detailed solution to problem 4.
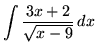 .
.
Click HERE to see a detailed solution to problem 5.
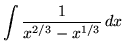 .
.
Click HERE to see a detailed solution to problem 6.
![$ \displaystyle{ \int { \sqrt{x} + 1 \over \sqrt{x} ( \sqrt[3] {x} + 1 ) } \, dx } $](img52.gif) .
.
Click HERE to see a detailed solution to problem 7.
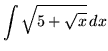 .
.
Click HERE to see a detailed solution to problem 8.
![$ \displaystyle{ \int \sqrt[3] { 1 + \sqrt{x-3} } \, dx } $](img54.gif) .
.
Click HERE to see a detailed solution to problem 9.
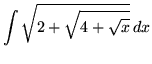 .
.
Click HERE to see a detailed solution to problem 10.
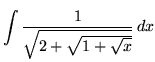 .
.
Click HERE to see a detailed solution to problem 11.
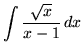 .
.
Click HERE to see a detailed solution to problem 12.
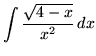 .
.
Click HERE to see a detailed solution to problem 13.
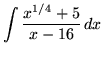 .
.
Click HERE to see a detailed solution to problem 14.
Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :