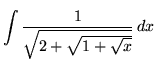 . Remove the ``outside" square root first. Use the power substitution
. Remove the ``outside" square root first. Use the power substitution
![]()
so that
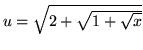
![]()
![]()
![]() ,
,
and (Use the chain rule.)
![]() ,
,
or
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
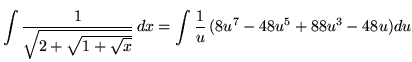
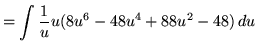

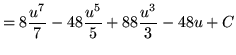

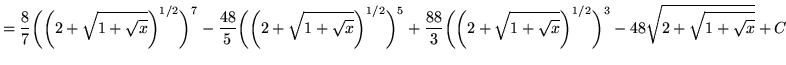
 .
.
Click HERE to return to the list of problems.
SOLUTION 12 : Integrate
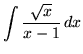 . Use the power substitution
. Use the power substitution
![]()
so that
![]()
and
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
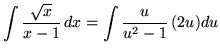
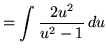
(Use polynomial division.)
 .
.
Use the method of partial fractions. Factor and decompose into partial fractions, getting
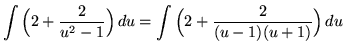
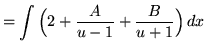
(After getting a common denominator, adding fractions, and equating numerators, it follows that
![]() ;
;
let
![]() ;
;
let
![]() .)
.)

![]()
![]()
(Recall that
![]() .)
.)
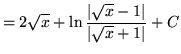 .
.
Click HERE to return to the list of problems.
SOLUTION 13 : Integrate
 . Use the power substitution
. Use the power substitution
![]()
so that
![]() ,
,
![]() ,
,
and
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting

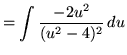 .
.
Use the method of partial fractions. Factor and decompose into partial fractions, getting (There are repeated linear factors!)

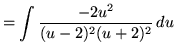
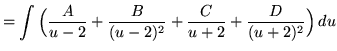
(After getting a common denominator, adding fractions, and equating numerators, it follows that
![]() ;
;
let
![]() ;
;
let
![]() ;
;
let
![]()
![]() ;
;
let
![]()
![]() ;
;
it follows that
![]() and
and
![]() .)
.)

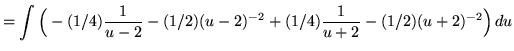

![]()
![]()
(Recall that
![]() .)
.)
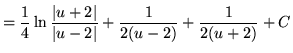
 .
.
Click HERE to return to the list of problems.
SOLUTION 14 : Integrate
 . Use the power substitution
. Use the power substitution
![]()
so that
![]()
and
![]() .
.
Substitute into the original problem, replacing all forms of ![]() , getting
, getting
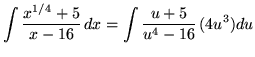

(Use polynomial division.)
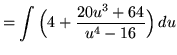 .
.
Use the method of partial fractions. Factor and decompose into partial fractions, getting
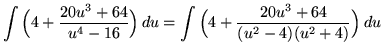
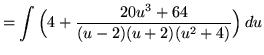
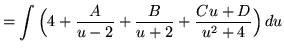
(After getting a common denominator, adding fractions, and equating numerators, it follows that
![]() ;
;
let
![]() ;
;
let
![]() ;
;
let
![]()
![]()
![]() ;
;
it follows that
![]() and
and
![]() and
and ![]() .)
.)
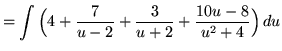


![]()

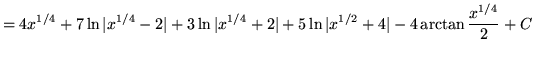 .
.
Click HERE to return to the list of problems.