Differentials Problems

Processing math: 36%

Solving Differentials Problems

The following problems involve the concept of the Differential of a Function. I will introduce the Differential via it's geometric interpretation and then formulate it. For a function $y=f(x)$ it will be shown that Differentials can be used to estimate the change of $y-$ values as a function of a change in $x$ -values. We will use Differentials to solve three types of problems. Differentials will be used to

$\ \ \ \ \$ I.) estimate the value of a numerical expression.
$\ \ \ \$ II.) approximate a relatively complicated functional expression with a simpler polynomial expression.
$\ \ \$ III.) estimate the propagation of percentage errors.

Let's begin with the graph of a function $y=f(x)$ and consider $x-$ values changing from $x$ to $x+ \Delta x$ , where $\Delta x$ will be used to represent a small positive or negative change in $x$ . I will refer to $x$ as the "starting" $x-$ value and to $x + \Delta x$ as the second $x-$ value. Draw a tangent line to this graph at $x$ .

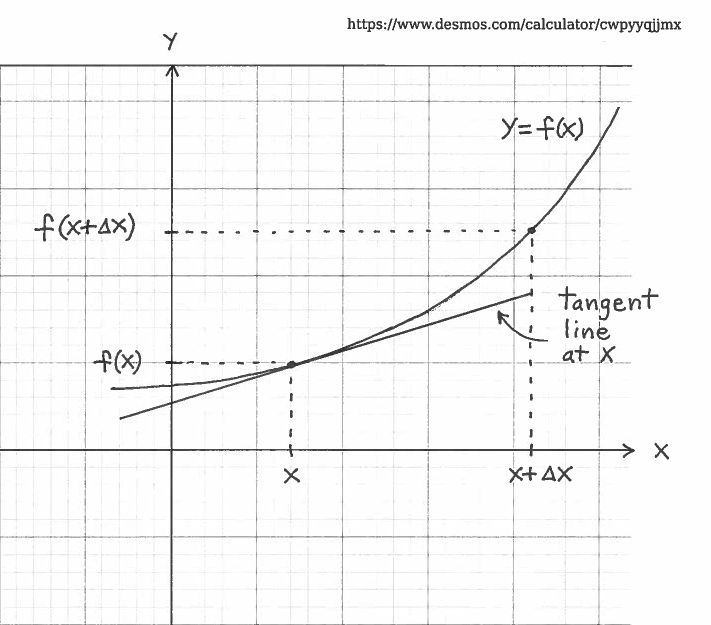
tex2html_wrap_inline125

Since

$x-$ values change from

$x$ to

$x+ \Delta x$ , the corresponding

$y-$ values will change from

$f(x)$ to

$f(x + \Delta x)$ . Define this exact change in

$y$ -values to be

$\Delta y$ , where

$\Delta y = f(x + \Delta x) - f(x)$ We can now geometrically define this so-called Differential of

$f(x)$ . We will denote the Differential by

$dy$ . It is the HEIGHT of the designated right triangle formed by

$x$ ,

$x+ \Delta x$ , and the tangent line to the graph of

$y=f(x)$ at

$x$ in the following diagram:

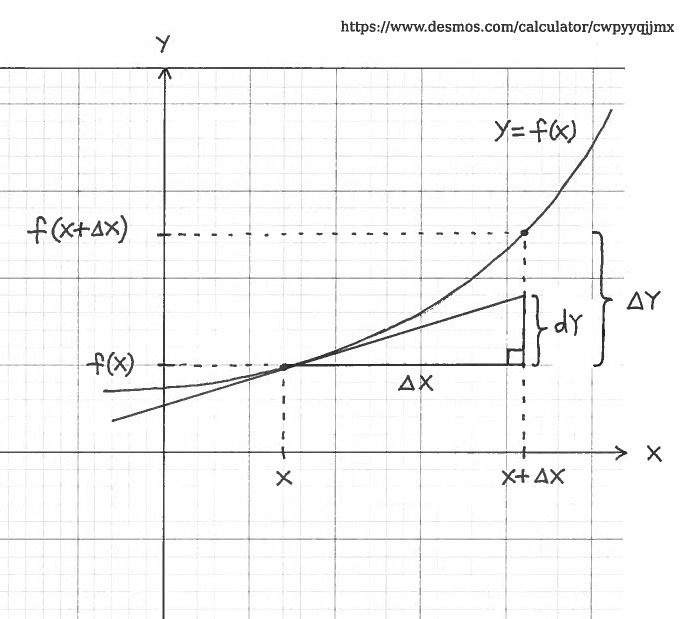
tex2html_wrap_inline125

Let's find a formula for

$dy$ . Recall from algebra that the SLOPE of this tangent line at

$x$ is

$m = \displaystyle{ rise \over run } = \displaystyle{ dy \over \Delta x }$ Recall also that the SLOPE of this tangent line at

$x$ is the derivative

$m=f'(x)$ Setting these slopes equal to each other gives us

$\displaystyle{ dy \over \Delta x } = f'(x)$

so that the Differential of Function

$f$ at

$x$ is

$dy = f'(x) \ \Delta x$

Let's now verify that the Exact Change of

$\ y=f(x) \$ is approximately equal to the Differential of

$\ y=f(x) \$ for "small"

$\Delta x$ , i.e.,

$\Delta y \approx dy$

for small

$\Delta x$ . Recall that the Derivative of

$f$ at

$x$ is

$\displaystyle{ \lim_{ \Delta x \to 0 } { f(x + \Delta x) - f(x) \over \Delta x } } = f'(x) \ \ \ \ \longrightarrow$

$\displaystyle{ { f(x + \Delta x) - f(x) \over \Delta x } } \approx f'(x) \ \ \ \ \longrightarrow$
for "small"

$\Delta x$

$\displaystyle{ { \Delta y \over \Delta x } } \approx f'(x) \ \ \ \ \longrightarrow$

$\Delta y \approx f'(x) \ \Delta x \ \ \ \ \longrightarrow$

$\Delta y \approx dy$
for "small"

$\Delta x$ .

Here is a summary of Differentials facts.

$\ \ \ \$ 1. Differentials require a function,

$y=f(x)$ .

$\ \ \ \$ 2. Differentials require two

$x-$ values, written as

$\ x-$ values:

$x \ \rightarrow x + \Delta x$ , where

$x$ is denoted as the "starting"

$x-$ value and

$\Delta x$ can be positive or negative.

$\ \ \ \$ 3. The Exact Change in

$y-$ values is

$\ \Delta y = f(x+ \Delta x)- f(x)$ .

$\ \ \ \$ 4. The Differential formula is

$\ dy = f'(x) \ \Delta x$ , where

$x$ is the "starting"

$x-$ value.

$\ \ \ \$ 5. We will assume that

$\ \Delta y \approx dy \$ if

$\Delta x$ is "small."

In the list of Differentials Problems which follows, most problems are average and a few are somewhat challenging.

CATEGORY I-- Using Differentials to Estimate the Value of a Numerical Expression

PROBLEM 1 : Use a Differential to estimate the value of $\ \sqrt{28}$ .

Click HERE to see a detailed solution to problem 1.
PROBLEM 2 : Use a Differential to estimate the value of $\ 10^{1/3}$ .

Click HERE to see a detailed solution to problem 2.
PROBLEM 3 : Use a Differential to estimate the value of $\ \sqrt{96}$ .

Click HERE to see a detailed solution to problem 3.
PROBLEM 4 : Use a Differential to estimate the value of $\ 14^{3/4}$ .
Click HERE to see a detailed solution to problem 4.
PROBLEM 5 : Use a Differential to estimate the value of $\ \sqrt{72}$ .

$\ \ \$ a.) Use 64 as a "starting" $x-$ value.
$\ \ \$ b.) Use 81 as a "starting" $x-$ value.

Click HERE to see a detailed solution to problem 5.
PROBLEM 6 : Use a Differential to estimate the value of $\ e^{-0.3}$ .

Click HERE to see a detailed solution to problem 6.
PROBLEM 7 : Use a Differential to estimate the value of $\ \ln(1.2)$ .

Click HERE to see a detailed solution to problem 7.
PROBLEM 8 : Use a Differential to estimate the value of $\ 30^{2/5}$ .

Click HERE to see a detailed solution to problem 8.
PROBLEM 9 : Use a Differential to estimate the value of $\ \tan( \displaystyle{ \pi \over 4 } + 0.15)$ .

Click HERE to see a detailed solution to problem 9.
PROBLEM 10 : Use a Differential to estimate the value of $\ \sin( \displaystyle{ \pi \over 6 } - 0.09)$ .

Click HERE to see a detailed solution to problem 10.
PROBLEM 11 : Use a Differential to estimate the value of $\ \arctan(1.1)$ .

Click HERE to see a detailed solution to problem 11.
PROBLEM 12 : Use a Differential to estimate the value of $\ \arcsin(0.45)$ .

Click HERE to see a detailed solution to problem 12.
PROBLEM 13 : Use a Differential to estimate the value of $\ \arcsin(0.12)$ .

Click HERE to see a detailed solution to problem 13.

CATEGORY II-- Using Differentials to Approximate a Relatively Complicated Functional Expression with a Simpler Polynomial Expression

PROBLEM 14 : Use a Differential to verify the following statement: $\ \ \ \ \sqrt{ 16+3h } \approx 4+ \displaystyle{ 3 \over 8 }h \ \$ for "small" $h$

Click HERE to see a detailed solution to problem 14.
PROBLEM 15 : Use a Differential to verify the following statement: $\ \ \ \ \displaystyle{ h^2 \over 4+h^2 } \approx \displaystyle{ 1 \over 4 }h^2 \ \$ for "small" $h$

Click HERE to see a detailed solution to problem 15.
PROBLEM 16 : Use a Differential to verify the following statement: $\ \ \ \ (8+5h^3)^{1/3} \approx 2+\displaystyle{ 5 \over 12 }h^3 \ \$ for "small" $h$

Click HERE to see a detailed solution to problem 16.
PROBLEM 17 : Use a Differential to verify the following statement: $\ \ \ \ \ln(4+7h) \approx \ln(4)+\displaystyle{ 7 \over 4 }h \ \$ for "small" $h$

Click HERE to see a detailed solution to problem 17.
PROBLEM 18 : Use a Differential to verify the following statement: $\ \ \ \ \log(100-h^4) \approx 2 - \displaystyle{ 1 \over 100 \ln(10) }h \ \$ for "small" $h$

Click HERE to see a detailed solution to problem 18.
PROBLEM 19 : Use a Differential to verify the following statement: $\ \ \ \ \sqrt{ 25+h^3-h^2 } \approx 5+ \displaystyle{ 1 \over 10 }h^3 - \displaystyle{ 1 \over 10 }h^2 \ \$ for "small" $h$

Click HERE to see a detailed solution to problem 19.
PROBLEM 20 : Use a Differential to verify the following statement: $\ \ \ \ \displaystyle{ 1 \over \sqrt{ 1-h^2 } } \approx 1 + \displaystyle{ 1 \over 2 }h^2 \ \$ for "small" $h$

Click HERE to see a detailed solution to problem 20.
PROBLEM 21 : Use a Differential to verify the following statement: $\ \ \ \ \displaystyle{ 8-h^2 \over (1+h^2)^2 } \approx 8-17h^2 \ \$ for "small" $h$

Click HERE to see a detailed solution to problem 21.

CATEGORY II-- Using Differentials to Approximate the Percentage Errors

For the following problems we will refer to

$|\Delta x|$ as the "absolute error in

$x$ and to

$|\Delta y|$ as the "absolute error in

$y$ . We will define

$\displaystyle{ |\Delta x| \over x }$ to be the "absolute percentage error in

$x$ " and

$\displaystyle{ |\Delta y| \over y }$ to be the "absolute percentage error in

$y$ ". For example, if

$\Delta x= -0.4$ and

$x=20$ , then the absolute percentage error in

$x$ is

$\displaystyle{ |-0.4| \over 20 }= { 0.4 \over 20 } = { 0.4 \over 20 }{ 5 \over 5} = { 2 \over 100 } = 2\%$

PROBLEM 22 : Assume that the edge of a square is measured with an absolute percentage error of at most $3\%$ . Use a differential to estimate the absolute percentage error in computing the square's

$\ \ \ \$ a.) $\ \$ perimeter.
$\ \ \ \$ b.) $\ \$ area.

Click HERE to see a detailed solution to problem 22.
PROBLEM 23 : Assume that the radius of a circle is measured with an absolute percentage error of at most $2\%$ . Use a differential to estimate the absolute percentage error in computing the circle's

$\ \ \ \$ a.) $\ \$ circumference.
$\ \ \ \$ b.) $\ \$ area.

Click HERE to see a detailed solution to problem 23.

CATEGORY III-- Miscellaneous Differential Problems

PROBLEM 24 : A large, juicy grapefruit is cut in half. The diameter of the circular cross-section of this grapefruit (not including the peel) is measured to be 10 inches. The peel is measured to be $1/4$ inch thick.

a.) Find the exact total volume of the entire peel.
b.) Use a Differential to estimate the volume of the entire peel.

Click HERE to see a detailed solution to problem 24.
PROBLEM 25 : A large angel food cake is in the shape of a cube of side length $30 \ cm$ . The entire cake is dipped in warm chocolate frosting resulting in a delicious coating of frosting $1/2 \ cm$ thick.

a.) Find the exact total volume of the frosting.
b.) Use a Differential to estimate the volume of the frosting.

Click HERE to see a detailed solution to problem 25.

Click HERE to return to the original list of various types of calculus problems.

Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :

kouba@math.ucdavis.edu

A heartfelt "Thank you" goes to The MathJax Consortium for making the construction of this webpage fun and easy.

Duane Kouba ... October 24, 2019