Areas of Enclosed Regions

COMPUTING THE AREAS OF ENCLOSED REGIONS USING VERTICAL OR HORIZONTAL CROSS-SECTIONS

The following problems involve the use of integrals to compute the area of two-dimensional plane regions. Integration can use either vertical cross-sections or horizontal cross-sections. Often one method is easier than the other. Sometimes both methods work easily. We will begin with a brief review of describing regions in the plane using vertical and horizontal cross-sections.

DESCRIBING REGIONS IN THE PLANE USING VERTICAL OR HORIZONTAL CROSS-SECTIONS

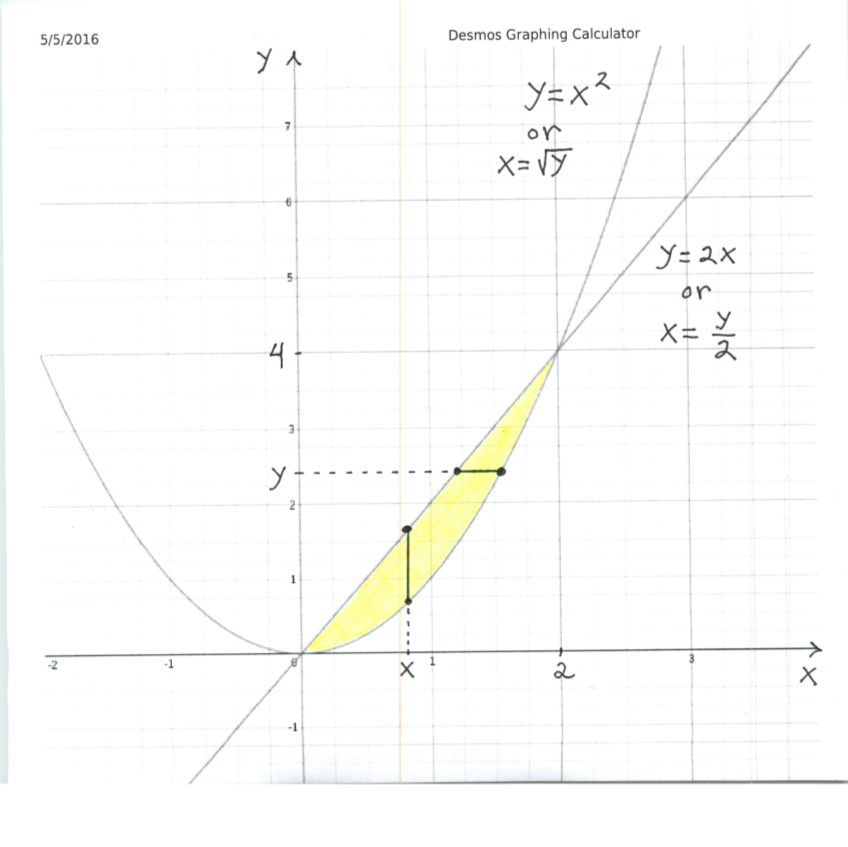
EXAMPLE 1: Consider the region in the plane enclosed by the graphs of $ y=2x $ and $ y= x^2 $. These graphs intersect when $ x=0 $ and $ x=2 $. Construct a vertical cross-section at $x$ for this region by FIRST picking a random value of $x$ between 0 and 2 and drawing a vertical line segment at $x$ starting from the graph of $ y=x^2 $ and ending on the graph of $ y=2x $ (See the graph below.). This region can now be described using vertical cross-sections as follows : $$ 0 \le x \le 2 \ \ and \ \ x^2 \le y \le 2x $$ Note that the equations $ y=x^2 $ and $ y=2x $ are equivalent to the equations $ x= \sqrt{y} $ and $ x= (1/2)y $, resp. Now construct a horizontal cross-section at $y$ for this region by FIRST picking a random value of $y$ between 0 and 4 and drawing a horizontal line segment at $y$ starting from the graph of $ x= (1/2)y $ and ending on the graph of $ x= \sqrt{y} $ (See the graph below.). This region can now be described using horizontal cross-sections as follows : $$ 0 \le y \le 4 \ \ and \ \ (1/2)y \le x \le \sqrt{y} $$

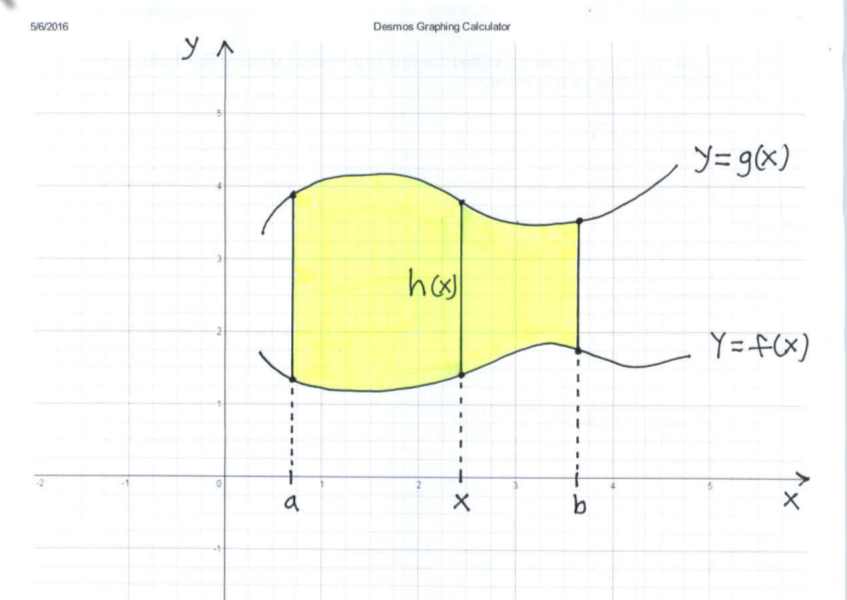
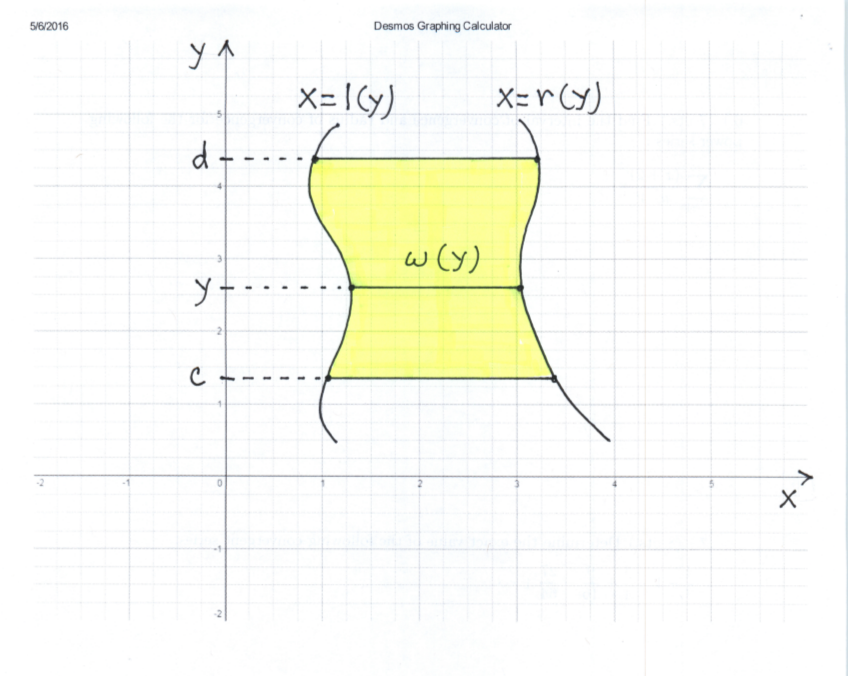
tex2html_wrap_inline125

COMPUTING THE AREAS OF REGIONS IN THE PLANE USING INTEGRATION

To find the area of a region in the plane we simply integrate the height, $h(x)$, of a vertical cross-section at $x$ or the width, $w(y)$, of a horizontal cross-section at $y$. The generalization for finding areas of regions in the plane follows.

If a region $R$ in the plane can be described using vertical cross-sections as $$ a \le x \le b \ \ and \ \ f(x) \le y \le g(x) $$ then the height of the vertical cross-section at $x$ is $ h(x) = Top - Bottom = g(x) - f(x) $ (See figure below.)

tex2html_wrap_inline125

and the area of $R$ is given by $$ AREA = \int_a^b h(x) \, dx = \int_a^b ( g(x) - f(x) ) \, dx $$ If a region $R$ in the plane can be described using horizontal cross-sections as $$ c \le y \le d \ \ and \ \ l(y) \le x \le r(y) $$ then the width of the horizontal cross-section at $y$ is $ w(y) = Right - Left = r(y) - l(y) $ (See figure below.)

tex2html_wrap_inline125

and the area of $R$ is given by $$ AREA = \int_c^d w(y) \, dy = \int_c^d ( r(y) - l(y) ) \, dy $$ EXAMPLE 2: Compute the area of the region in the plane enclosed by the graphs of $ y=2x $ and $ y= x^2 $. Using vertical cross-sections we have that $$ 0 \le x \le 2 \ \ and \ \ x^2 \le y \le 2x $$ so that the area of the region is $$ AREA = \int_0^2 h(x) \, dx = \int_0^2 ( Top - Bottom ) \, dx $$ $$ = \int_0^2 ( 2x-x^2 ) \, dx $$ $$ = (x^2-(1/3)x^3) \Big\vert_{0}^{2} $$ $$ = 4 - 8/3 $$ $$ = 4/3 $$ Using horizontal cross-sections we have that $$ 0 \le y \le 4 \ \ and \ \ (1/2)y \le x \le \sqrt{y} $$ so that the area of the region is $$ AREA = \int_0^4 w(y) \, dy = \int_0^4 ( Right - Left ) \, dy $$ $$ = \int_0^4 ( \sqrt{y} - (1/2)y ) \, dy $$ $$ = ( (2/3)x^{3/2}- (1/4)y^2 ) \Big\vert_{0}^{4} $$ $$ = (2/3)4^{3/2}- (1/4)4^2 $$ $$ = (2/3)(8)- (1/4)(16) $$ $$ = 16/3- 4 $$ $$ = 4/3 $$

The following problems use integration to find areas of regions in the plane. Most are average. A few are somewhat challenging. It's arguable that the most important component in getting the correct solutions to the following problems is a carefully and completely detailed graph of the enclosed region. This includes proper labeling of the axes, graphs, intercepts, and cross-sections.

Compute the area of the region enclosed by the graphs of the given equations. Use vertical cross-sections on Problems 1-16.

PROBLEM 1 : $ y=x, y=2x, $ and $ x=4 $
Click HERE to see a detailed solution to problem 1.
PROBLEM 2 : $ y=x^2 $ and $ y=x+2 $
Click HERE to see a detailed solution to problem 2.
PROBLEM 3 : $ y=e^x, y=e^{-x}, $ and $ x= \ln 3 $
Click HERE to see a detailed solution to problem 3.
PROBLEM 4 : $ y=x^2$ and $ y=-x^2+4x+6 $
Click HERE to see a detailed solution to problem 4.
PROBLEM 5 : $ y=x^3+x^2$ and $ y=3x^2+3x $
Click HERE to see a detailed solution to problem 5.
PROBLEM 6 : $ y= \ln x, y=1, $ and $ x=e^2 $
Click HERE to see a detailed solution to problem 6.
PROBLEM 7 : $ y= \cos x, y= \sin x, $ and $ x=0 $
Click HERE to see a detailed solution to problem 7.
PROBLEM 8 : $ y=8/x, y=2x, $ and $ y=2 $
Click HERE to see a detailed solution to problem 8.
PROBLEM 9 : $ y=\ln x $ and $ y= (\ln x)^2 $
Click HERE to see a detailed solution to problem 9.
PROBLEM 10 : $ y=\tan^2 x, y=0, $ and $ x=1 $
Click HERE to see a detailed solution to problem 10.
PROBLEM 11 : $ y=x, y=2x, $ and $ y=6-x $
Click HERE to see a detailed solution to problem 11.
PROBLEM 12 : $ y=\sin \sqrt{x}$ and $ y=0 $ on the interval $ [0, \pi^2] $
Click HERE to see a detailed solution to problem 12.
PROBLEM 13 : $ y=x^3 $ and $ y=4x$
Click HERE to see a detailed solution to problem 13.
PROBLEM 14 : $ y=\displaystyle \frac{1}{4}x^4-x^2 $ and $ y=x(x-2)(x+2) $
Click HERE to see a detailed solution to problem 14.
PROBLEM 15 : $ y=\sin x $ and $ \sin 2x $ on the interval $ [0, \pi] $
Click HERE to see a detailed solution to problem 15.
PROBLEM 16 : $ y=2x $ and $ y= \displaystyle{ 1 \over 2 }x-4 $ , $ y=0 $, and $ y=2 $.
Click HERE to see a detailed solution to problem 16.

Compute the area of the region enclosed by the graphs of the given equations. Use horizontal cross-sections on Problems 17-22.

PROBLEM 17 : $ x=y^2 $ and $ x=4 $
Click HERE to see a detailed solution to problem 17.
PROBLEM 18 : $ x=y+3 $ and $ x=y^2-y $
Click HERE to see a detailed solution to problem 18.
PROBLEM 19 : $ x=y^3 $ and $ x=y^2+2y $
Click HERE to see a detailed solution to problem 19.
PROBLEM 20 : $ y= \displaystyle\frac{2}{x}, y= \frac{1}{2}x, $ and $ y=2 $
Click HERE to see a detailed solution to problem 20.
PROBLEM 21 : $ y= \tan x, y=x, $ and BELOW $ y=3 $
Click HERE to see a detailed solution to problem 21.
PROBLEM 22 : $ y=2x $ and $ y= \displaystyle{ 1 \over 2 }x-4 $ , $ y=0 $, and $ y=2 $
Click HERE to see a detailed solution to problem 22.

In Problems 23-28 compute the area of the region enclosed by the graphs of the given equations. Use a.) vertical cross-sections and b.) horizontal cross-sections. SET UP BUT DO NOT EVALUATE THE INTEGRALS.

PROBLEM 23 : $ y= 3x, y=x, $ and $ x=2 $
Click HERE to see a detailed solution to problem 23.
PROBLEM 24 : $ y= 2x, y=\displaystyle \frac{1}{2}x, $ and $ y=4 $
Click HERE to see a detailed solution to problem 24.
PROBLEM 25 : $ x=y^2 $ and $ x=y+2 $
Click HERE to see a detailed solution to problem 25.
PROBLEM 26 : $ y=e^x, y=e^{-x}, $ and $ x=2 $
Click HERE to see a detailed solution to problem 26.
PROBLEM 27 : $ y= \ln x, y=1-x, $ and $ y=2 $
Click HERE to see a detailed solution to problem 27.
PROBLEM 28 : $ y=x^3, y=x+6, y=2x-6,$ and $ y=0 $
Click HERE to see a detailed solution to problem 28.
PROBLEM 29 : $ y=x^2-2x+2$ and $ y=2x+2 $
Click HERE to see a detailed solution to problem 29.

Click HERE to return to the original list of various types of calculus problems.

Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :

kouba@math.ucdavis.edu

A heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easy.

Duane Kouba ... May 6, 2016